Chào mừng các em học sinh đến với lời giải chi tiết bài tập 5 trang 51 SGK Toán 9 tập 2 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập Toán 9.
Bài tập 5 trang 51 thuộc chương trình học Toán 9 tập 2, tập trung vào việc rèn luyện kỹ năng giải bài toán thực tế và áp dụng các công thức đã học.
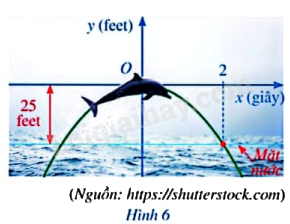
Cá heo có thể nhảy cao tới 25 feet và thực hiện các thủ thuật như nhảy qua vòng, lộn nhào trong không trung. Giả sử quỹ đạo nhảy của cá heo là parabol (y = a{x^2}), với gốc tọa độ là vị trí cao nhất mà cá heo đạt được, cách mặt nước 25 feet, trong đó y được tính theo đơn vị feet và x được tính theo đơn vị giây (Hình 6). Biết rằng sau 2 giây kể từ vị trí cao nhất đó, cá heo rơi chạm mặt nước. tìm hàm số biểu thị quỹ đạo nhảy của cá heo.
Đề bài
Cá heo có thể nhảy cao tới 25 feet và thực hiện các thủ thuật như nhảy qua vòng, lộn nhào trong không trung. Giả sử quỹ đạo nhảy của cá heo là parabol \(y = a{x^2}\), với gốc tọa độ là vị trí cao nhất mà cá heo đạt được, cách mặt nước 25 feet, trong đó y được tính theo đơn vị feet và x được tính theo đơn vị giây (Hình 6). Biết rằng sau 2 giây kể từ vị trí cao nhất đó, cá heo rơi chạm mặt nước. tìm hàm số biểu thị quỹ đạo nhảy của cá heo.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Xác định giá trị của x và y sau đó thay vào hàm số \(y = a{x^2}\) để tìm a.
Lời giải chi tiết
Ta thấy quỹ đạo nhảy của cá heo là parabol có vị trí cao nhất là O(0;0) suy ra đồ thị nằm bên dưới trục hoành và y = -25 và x = 2.
Thay y = -25 và x = 2 vào hàm số \(y = a{x^2}\) ta được: \( - 25 = a{.2^2} \Leftrightarrow a = \frac{{ - 25}}{4}\)
Vậy hàm số biểu thị quỹ đạo nhảy của cá heo có dạng \(y = \frac{{ - 25}}{4}{x^2}\).
Bài tập 5 trang 51 SGK Toán 9 tập 2 - Cánh diều là một bài tập quan trọng trong chương trình học Toán 9, yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Dưới đây là hướng dẫn chi tiết cách giải bài tập này, giúp các em hiểu rõ bản chất và phương pháp giải.
Trước khi bắt đầu giải bài tập, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Bài tập 5 trang 51 thường yêu cầu học sinh:
Để giải bài tập 5 trang 51 SGK Toán 9 tập 2 - Cánh diều, chúng ta có thể áp dụng các phương pháp sau:
Bài tập 5: Cho hàm số y = 2x + 3. Hãy tìm các điểm thuộc đồ thị hàm số có hoành độ là -2, 0, 1.
Lời giải:
Ví dụ: Cho hàm số y = x2 - 4x + 3. Hãy tìm tọa độ đỉnh của parabol.
Lời giải:
Hàm số y = x2 - 4x + 3 có dạng y = ax2 + bx + c, với a = 1, b = -4, c = 3.
Hoành độ đỉnh của parabol là x0 = -b / (2a) = -(-4) / (2*1) = 2.
Tung độ đỉnh của parabol là y0 = a*x02 + b*x0 + c = 1*(2)2 - 4*2 + 3 = -1.
Vậy tọa độ đỉnh của parabol là (2, -1).
Để nắm vững kiến thức và kỹ năng giải bài tập 5 trang 51 SGK Toán 9 tập 2 - Cánh diều, các em nên luyện tập thêm các bài tập tương tự. Dưới đây là một số bài tập gợi ý:
Bài tập 5 trang 51 SGK Toán 9 tập 2 - Cánh diều là một bài tập quan trọng, giúp các em rèn luyện kỹ năng giải bài toán về hàm số bậc nhất và hàm số bậc hai. Hy vọng với hướng dẫn chi tiết và dễ hiểu trên đây, các em sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán.
Chúc các em học tập tốt!