Chào mừng bạn đến với bài học về Lý thuyết Tần số và Tần số tương đối trong chương trình Toán 9 Cánh diều. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về chủ đề này.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, công thức tính toán và các ứng dụng thực tế của Tần số và Tần số tương đối, giúp bạn giải quyết các bài tập một cách hiệu quả.
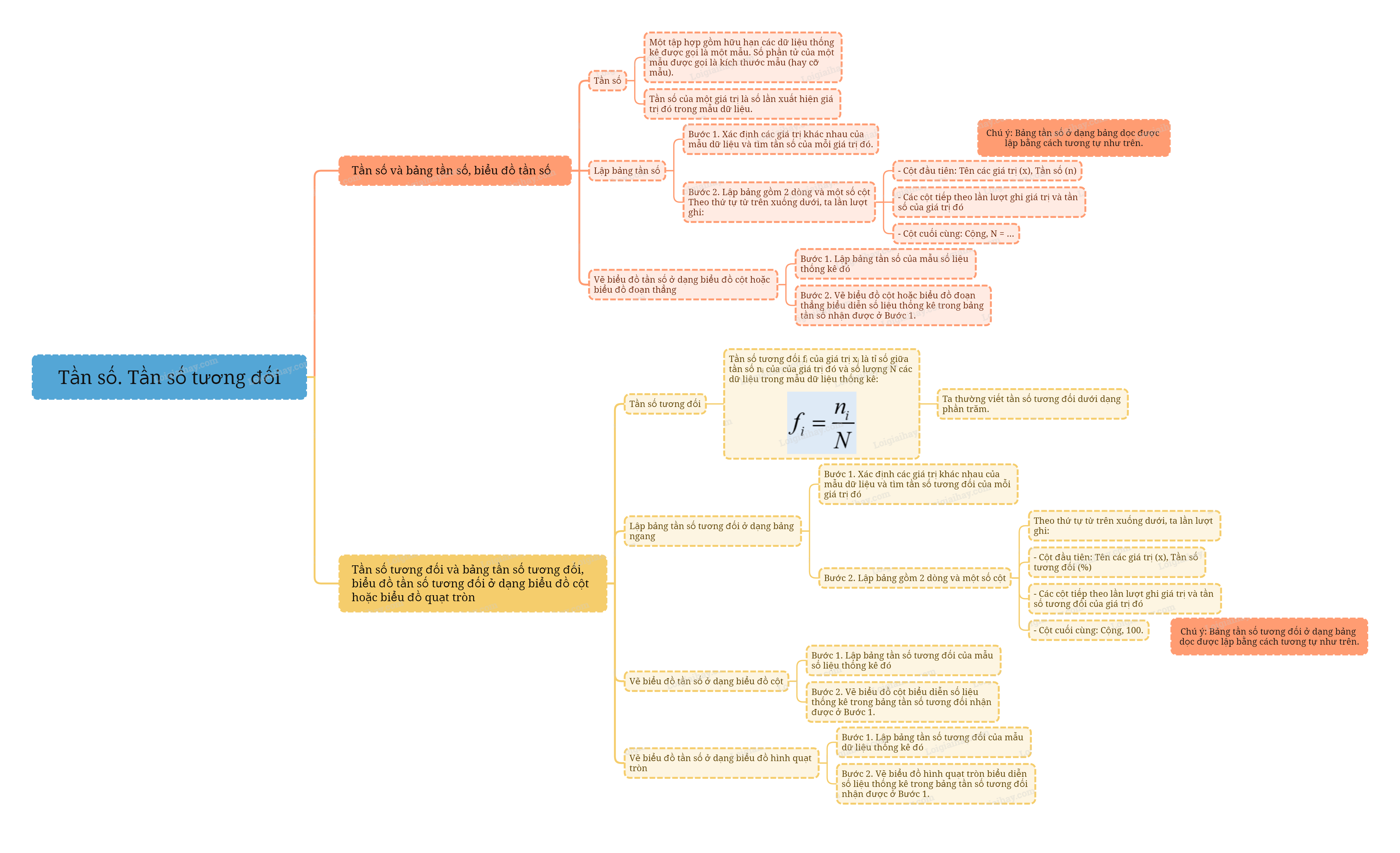
1. Tần số và bảng tần số, biểu đồ tần số Tần số Một tập hợp gồm hữu hạn các dữ liệu thống kê được gọi là một mẫu. Số phần tử của một mẫu được gọi là kích thước mẫu (hay cỡ mẫu). Tần số của một giá trị là số lần xuất hiện giá trị đó trong mẫu dữ liệu.
1. Tần số và bảng tần số, biểu đồ tần số
Tần số
Một tập hợp gồm hữu hạn các dữ liệu thống kê được gọi là một mẫu. Số phần tử của một mẫu được gọi là kích thước mẫu (hay cỡ mẫu). Tần số của một giá trị là số lần xuất hiện giá trị đó trong mẫu dữ liệu. |
Lập bảng tần số
Để lập bảng tần số ở dạng bảng ngang, ta có thể làm như sau: Bước 1. Xác định các giá trị khác nhau của mẫu dữ liệu và tìm tần số của mỗi giá trị đó. Bước 2. Lập bảng gồm 2 dòng và một số cột Theo thứ tự từ trên xuống dưới, ta lần lượt ghi: - Cột đầu tiên: Tên các giá trị (x), Tần số (n) - Các cột tiếp theo lần lượt ghi giá trị và tần số của giá trị đó - Cột cuối cùng: Cộng, N = ... Chú ý:Bảng tần số ở dạng bảng dọc được lập bằng cách tương tự như trên. |
Ví dụ: Thống kê khối lượng rau thu hoạch một vụ (đơn vị: tạ) của mỗi hộ gia đình trong 38 hộ gia đình tham gia chương trình trồng rau theo tiêu chuẩn VIETGAP như sau:

Trong 38 số liệu thống kê ở trên có 7 giá trị khác nhau là:
\({x_1} = 4;{x_2} = 5;{x_3} = 6;{x_4} = 7;{x_5} = 8;{x_6} = 9;{x_7} = 10\)
Tần số của giá trị \({x_1},{x_2},{x_3},{x_4},{x_5},{x_6},{x_7}\) lần lượt là:
\({m_1} = 4;{m_2} = 7;{m_3} = 5;{m_4} = 8;{m_5} = 7;{m_6} = 5;{m_7} = 2\).
Bảng tần số của mẫu số liệu thống kê là:

Vẽ biểu đồ tần số ở dạng biểu đồ cột hoặc biểu đồ đoạn thẳng
Bước 1. Lập bảng tần số của mẫu số liệu thống kê đó Bước 2. Vẽ biểu đồ cột hoặc biểu đồ đoạn thẳng biểu diễn số liệu thống kê trong bảng tần số nhận được ở Bước 1. |
Ví dụ: Biểu đồ tần số của mẫu số thống kê trong bảng tần số sau:
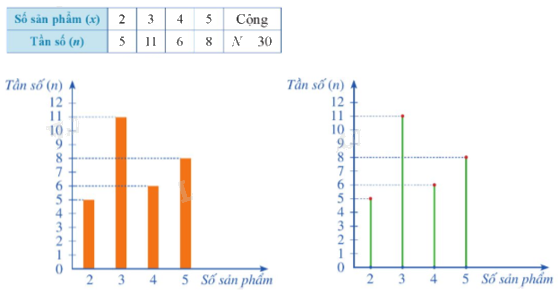
2. Tần số tương đối và bảng tần số tương đối, biểu đồ tần số tương đối ở dạng biểu đồ cột hoặc biểu đồ quạt tròn
Tần số tương đối
Tần số tương đối \({f_i}\) của giá trị \({x_i}\) là tỉ số giữa tần số \({n_i}\) của của giá trị đó và số lượng N các dữ liệu trong mẫu dữ liệu thống kê: \({f_i} = \frac{{{n_i}}}{N}\). Ta thường viết tần số tương đối dưới dạng phần trăm. |
Lập bảng tần số tương đối ở dạng bảng ngang
Bước 1. Xác định các giá trị khác nhau của mẫu dữ liệu và tìm tần số tương đối của mỗi giá trị đó Bước 2. Lập bảng gồm 2 dòng và một số cột Theo thứ tự từ trên xuống dưới, ta lần lượt ghi: - Cột đầu tiên: Tên các giá trị (x), Tần số tương đối (%) - Các cột tiếp theo lần lượt ghi giá trị và tần số tương đối của giá trị đó - Cột cuối cùng: Cộng, 100. Chú ý: Bảng tần số tương đối ở dạng bảng dọc được lập bằng cách tương tự như trên. |
Ví dụ: Cho bảng thống kê số anh, chị, em ruột của các bạn trong lớp:

Tổng số bạn là \(n = 30\).
Số anh, chị, em ruột là \({x_1} = 0;{x_2} = 1;{x_3} = 2;{x_4} = 3\) tương ứng với \({m_1} = 8;{m_2} = 12;{m_3} = 6,{m_4} = 4\).
Do đó các tần số tương đối cho các giá trị \({x_1},{x_2},{x_3},{x_4}\) lần lượt là:
\({f_1} = \frac{8}{{30}} \approx 26,7\% ;{f_2} = \frac{{12}}{{30}} = 40\% ;{f_3} = \frac{6}{{30}} = 20\% ;{f_4} = \frac{4}{{30}} \approx 13,3\% \).
Ta có bảng tần số tương đối sau:

Vẽ biểu đồ tần số ở dạng biểu đồ cột
Để vẽ biểu đồ tần số tương đối ở dạng biểu đồ cột của một mẫu dữ liệu thống kê, ta có thể thực hiện các bước sau: Bước 1. Lập bảng tần số tương đối của mẫu số liệu thống kê đó Bước 2. Vẽ biểu đồ cột biểu diễn số liệu thống kê trong bảng tần số tương đối nhận được ở Bước 1. |
Vẽ biểu đồ tần số ở dạng biểu đồ hình quạt tròn
Để vẽ biểu đồ tần số tương đối ở dạng biểu đồ hình quạt tròn của một mẫu dữ liệu thống kê, ta có thể thực hiện các bước sau: Bước 1. Lập bảng tần số tương đối của mẫu dữ liệu thống kê đó Bước 2. Vẽ biểu đồ hình quạt tròn biểu diễn số liệu thống kê trong bảng tần số tương đối nhận được ở Bước 1. |
Ví dụ: Cho bảng tần số tương đối về loại phim yêu thích của các học sinh trong lớp 9A như sau:

Biểu đồ tần số tương đối ở dạng biểu đồ cột của mẫu số liệu thống kê đó là:
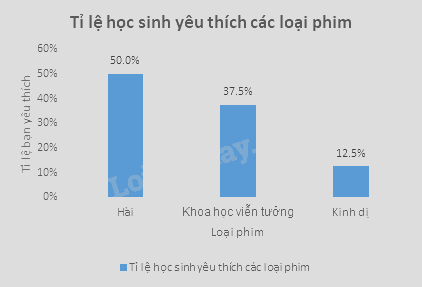
Biểu đồ tần số tương đối ở dạng biểu đồ hình quạt tròn của mẫu số liệu thống kê đó là:
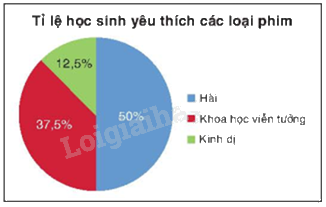
Trong chương trình Toán 9, phần thống kê và xác suất đóng vai trò quan trọng trong việc giúp học sinh hiểu và phân tích dữ liệu. Một trong những khái niệm cơ bản nhất của phần này là Tần số và Tần số tương đối. Bài viết này sẽ trình bày chi tiết về lý thuyết này, cùng với các ví dụ minh họa để giúp bạn nắm vững kiến thức.
Tần số của một giá trị trong một tập dữ liệu là số lần giá trị đó xuất hiện trong tập dữ liệu. Ví dụ, nếu chúng ta có một tập dữ liệu về điểm kiểm tra của 10 học sinh: 7, 8, 9, 7, 6, 8, 7, 9, 10, 8. Thì:
Tần số tương đối của một giá trị là tỷ lệ giữa tần số của giá trị đó và tổng số các giá trị trong tập dữ liệu. Công thức tính tần số tương đối là:
Tần số tương đối = (Tần số của giá trị) / (Tổng số các giá trị)
Sử dụng tập dữ liệu điểm kiểm tra ở trên, ta có:
Tần số và tần số tương đối giúp chúng ta:
Ví dụ 1: Một cửa hàng bán lẻ ghi lại số lượng sản phẩm bán được mỗi ngày trong một tuần:
| Ngày | Số lượng sản phẩm bán được |
|---|---|
| Thứ Hai | 20 |
| Thứ Ba | 25 |
| Thứ Tư | 18 |
| Thứ Năm | 22 |
| Thứ Sáu | 30 |
| Thứ Bảy | 35 |
| Chủ Nhật | 28 |
Tính tần số và tần số tương đối của số lượng sản phẩm bán được mỗi ngày.
Giải:
Ví dụ 2: Khảo sát về màu sắc yêu thích của học sinh lớp 9, kết quả thu được như sau:
Tính tần số tương đối của mỗi màu sắc.
Giải:
Tổng số học sinh được khảo sát: 15 + 20 + 10 + 5 = 50
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về Lý thuyết Tần số và Tần số tương đối trong Toán 9 Cánh diều. Chúc bạn học tập tốt!