Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 4 trang 34 sách giáo khoa Toán 9 tập 2 - Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp các em học sinh nắm vững kiến thức và đạt kết quả cao trong môn Toán.
Một cửa hàng sách thống kê số tiền (đơn vị: nghìn đồng) mà 60 khách hàng mua sách ở cửa hàng đó trong một ngày. Số liệu được ghi lại trong biểu đồ tần số ghép nhóm ở Hình 24: a) Lập bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó. b) Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột và biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm đó.
Đề bài
Một cửa hàng sách thống kê số tiền (đơn vị: nghìn đồng) mà 60 khách hàng mua sách ở cửa hàng đó trong một ngày. Số liệu được ghi lại trong biểu đồ tần số ghép nhóm ở Hình 24:
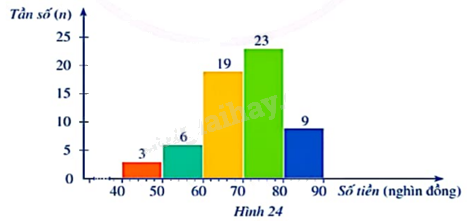
a) Lập bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó.
b) Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột và biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm đó.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Tính tỉ số phần trăm của mỗi tần số.
Lời giải chi tiết
a) Tần số tương đối của các nhóm lần lượt là:
\(\begin{array}{l}{f_1} = \frac{3}{{60}}.100\% = 5\% ;{f_2} = \frac{6}{{60}}.100\% = 10\% ;{f_3} = \frac{{19}}{{60}}.100\% = 31,7\% ;\\{f_4} = \frac{{23}}{{60}}.100\% = 38,3\% ;{f_5} = \frac{9}{{60}}.100\% = 15\% \end{array}\)
b) Ta có bảng:

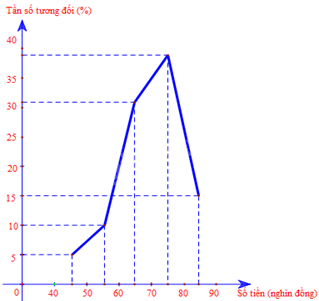
Biểu đồ đoạn thẳng:
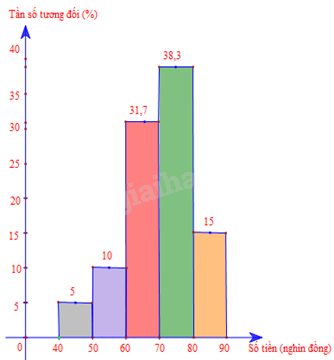
Biểu đồ cột:
Bài tập 4 trang 34 SGK Toán 9 tập 2 - Cánh diều thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:
Trước khi bắt đầu giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Bài tập 4 trang 34 SGK Toán 9 tập 2 - Cánh diều thường yêu cầu học sinh:
Để giải bài tập 4 trang 34 SGK Toán 9 tập 2 - Cánh diều, chúng ta có thể thực hiện theo các bước sau:
Giả sử đề bài yêu cầu chúng ta tìm hàm số bậc nhất đi qua hai điểm A(1; 2) và B(2; 4). Chúng ta có thể giải bài toán này như sau:
Bước 1: Xác định hàm số bậc nhất. Hàm số bậc nhất có dạng y = ax + b.
Bước 2: Tìm hệ số a và b của hàm số. Vì hàm số đi qua hai điểm A(1; 2) và B(2; 4), chúng ta có thể thay tọa độ của hai điểm này vào phương trình hàm số để được hai phương trình:
Giải hệ phương trình này, chúng ta được a = 2 và b = 0. Vậy hàm số bậc nhất cần tìm là y = 2x.
Bước 3: Vẽ đồ thị hàm số. Để vẽ đồ thị hàm số y = 2x, chúng ta cần xác định ít nhất hai điểm thuộc đồ thị hàm số. Ví dụ, chúng ta có thể chọn hai điểm A(0; 0) và B(1; 2). Sau đó, chúng ta nối hai điểm này lại với nhau để được đồ thị hàm số.
Khi giải bài tập về hàm số bậc nhất, chúng ta cần lưu ý một số điều sau:
Để củng cố kiến thức về hàm số bậc nhất, bạn có thể làm thêm một số bài tập sau:
Hy vọng rằng với hướng dẫn chi tiết này, bạn đã có thể giải bài tập 4 trang 34 SGK Toán 9 tập 2 - Cánh diều một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!