Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 4 trang 51 SGK Toán 9 tập 2 - Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Cho hàm số (y = a{t^2}) biểu thị quãng đường (đơn vị: mét) mà một chiếc xe đua đi được trong khoảng thời gian t (giây). Giả sử một chiếc xe đua đi được 125m sau khoảng thời gian là 5 giây. a) Tìm hệ số a. b) Vẽ đồ thị của hàm số.
Đề bài
Cho hàm số \(y = a{t^2}\) biểu thị quãng đường (đơn vị: mét) mà một chiếc xe đua đi được trong khoảng thời gian t (giây). Giả sử một chiếc xe đua đi được 125m sau khoảng thời gian là 5 giây.
a) Tìm hệ số a.
b) Vẽ đồ thị của hàm số.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Thay \(y = 125,t = 5\) vào hàm số \(y = a{t^2}\) để tìm a.
b) Xác định 5 điểm thuộc đồ thị hàm số, sau đó vẽ đường cong parabol đi qua 5 điểm đó.
Lời giải chi tiết
a) Thay \(y = 125,t = 5\) vào hàm số \(y = a{t^2}\) ta được:
\(125 = a{.5^2} \Leftrightarrow a = 5\)
Hàm số có dạng \(y = 5{t^2}\).
b) Ta có bảng:
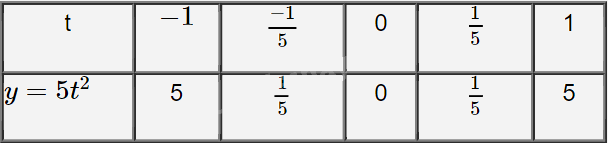
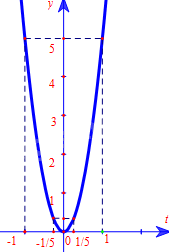
Đồ thị hàm số \(y = 5{t^2}\) là một parabol đi qua 5 điểm \(\left( { - 1;5} \right),(\frac{{ - 1}}{5};\frac{1}{5});\left( {0;0} \right),\left( {\frac{1}{5};\frac{1}{5}} \right),\left( {1;5} \right)\)
Bài tập 4 trang 51 SGK Toán 9 tập 2 - Cánh diều thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:
Cho hàm số y = (m-1)x + 3. Tìm giá trị của m để hàm số đồng biến.
Để hàm số y = ax + b đồng biến, điều kiện cần và đủ là a > 0. Trong trường hợp này, a = m - 1. Do đó, để hàm số y = (m-1)x + 3 đồng biến, ta cần có m - 1 > 0.
Giải bất phương trình m - 1 > 0, ta được m > 1.
Vậy, để hàm số y = (m-1)x + 3 đồng biến, thì m > 1.
Ví dụ 1: Nếu m = 2, thì hàm số trở thành y = x + 3. Hàm số này đồng biến vì hệ số của x là 1 > 0.
Ví dụ 2: Nếu m = 0, thì hàm số trở thành y = -x + 3. Hàm số này nghịch biến vì hệ số của x là -1 < 0.
Hàm số bậc nhất có nhiều ứng dụng trong thực tế, ví dụ như tính chi phí sản xuất, tính lợi nhuận, tính quãng đường đi được,… Việc nắm vững kiến thức về hàm số bậc nhất sẽ giúp bạn giải quyết các bài toán thực tế một cách dễ dàng hơn.
Bài tập 4 trang 51 SGK Toán 9 tập 2 - Cánh diều là một bài tập cơ bản về hàm số bậc nhất. Để giải bài tập này, bạn cần nắm vững điều kiện đồng biến, nghịch biến của hàm số bậc nhất. Hy vọng với hướng dẫn chi tiết này, bạn đã có thể giải bài tập này một cách thành công.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Chúc bạn học tập tốt!
| Điều kiện | Hàm số |
|---|---|
| a > 0 | Đồng biến |
| a < 0 | Nghịch biến |
| a = 0 | Hàm số hằng |
| Bảng tóm tắt điều kiện đồng biến, nghịch biến của hàm số y = ax + b | |