Chào mừng bạn đến với bài học về lý thuyết Tần số ghép nhóm và tần số tương đối ghép nhóm trong chương trình Toán 9 Cánh diều. Đây là một phần kiến thức quan trọng trong chương trình thống kê và xử lý dữ liệu.
Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản về cách tổ chức, phân tích dữ liệu và rút ra những kết luận hữu ích. Chúng ta sẽ cùng nhau tìm hiểu các khái niệm, công thức và ví dụ minh họa để bạn có thể áp dụng vào giải các bài tập thực tế.
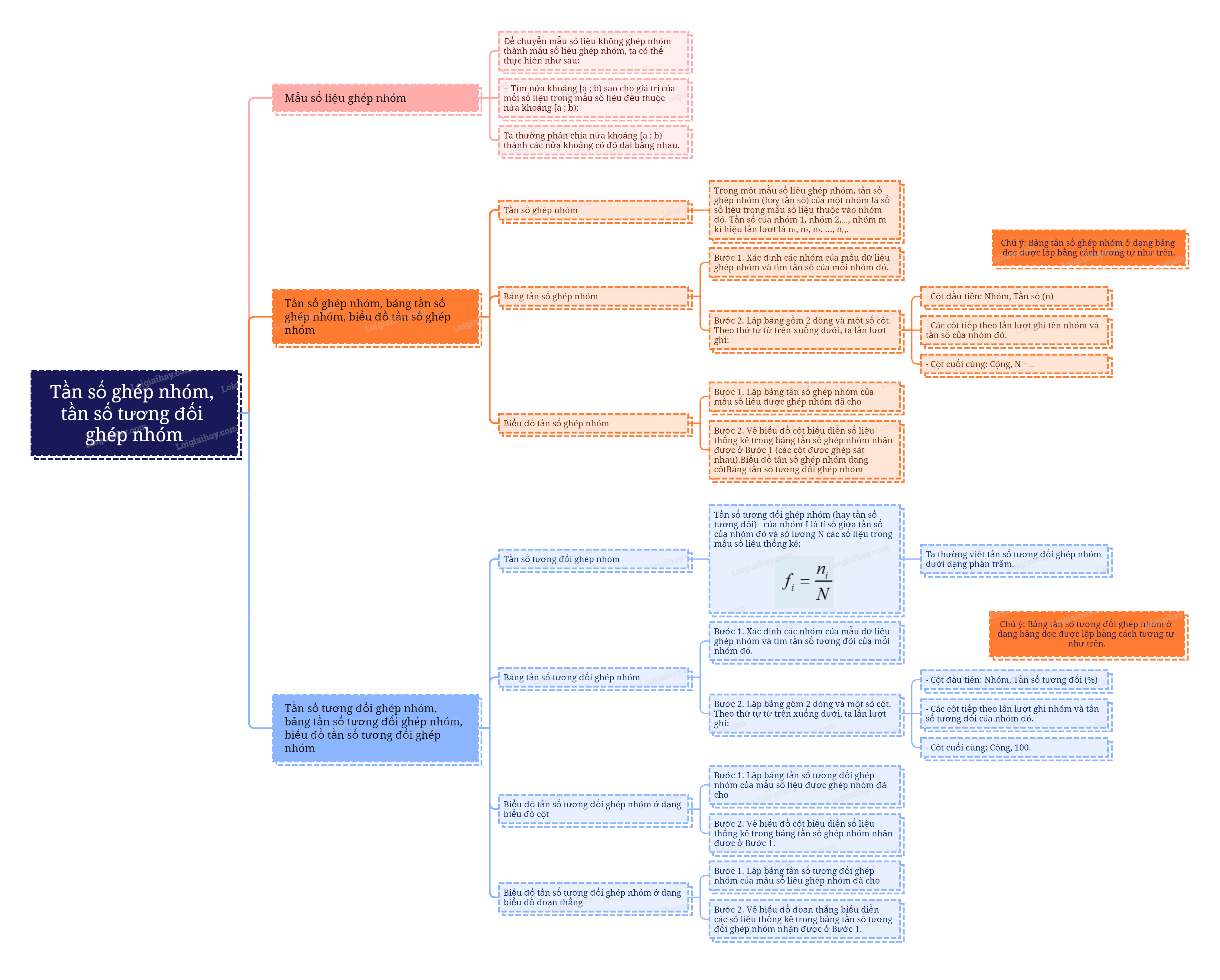
1. Mẫu số liệu ghép nhóm Để chuyển mẫu số liệu không ghép nhóm thành mẫu số liệu ghép nhóm, ta có thể thực hiện như sau: − Tìm nửa khoảng [a ; b) sao cho giá trị của mỗi số liệu trong mẫu số liệu đều thuộc nửa khoảng [a ; b); Ta thường phân chia nửa khoảng [a ; b) thành các nửa khoảng có độ dài bằng nhau.
1. Mẫu số liệu ghép nhóm
Để chuyển mẫu số liệu không ghép nhóm thành mẫu số liệu ghép nhóm, ta có thể thực hiện như sau: − Tìm nửa khoảng [a ; b) sao cho giá trị của mỗi số liệu trong mẫu số liệu đều thuộc nửa khoảng [a ; b); Ta thường phân chia nửa khoảng [a ; b) thành các nửa khoảng có độ dài bằng nhau. |
Chú ý: Khi ghép nhóm số liệu, đầu mút của các nhóm có thể không phải là giá trị của mẫu số liệu.
Ví dụ: Với mẫu số liệu chiều cao (đơn vị là cm) của học sinh lớp 9A như sau:

Số liệu có giá trị nhỏ nhất là 155, số liệu có giá trị lớn nhất là 166 , vì thế ta chọn nửa khoảng [155; 167).
Vì độ dài nửa khoảng bằng 167 – 155 = 12 nên ta có thể phân chia nửa khoảng đó thành sáu nửa khoảng có độ dài bằng nhau là: [155; 158), [158; 161), [161; 164), [164;167).
2. Tần số ghép nhóm, bảng tần số ghép nhóm, biểu đồ tần số ghép nhóm
Tần số ghép nhóm
Trong một mẫu số liệu ghép nhóm, tần số ghép nhóm (hay tần số) của một nhóm là số số liệu trong mẫu số liệu thuộc vào nhóm đó. Tần số của nhóm 1, nhóm 2,…, nhóm m kí hiệu lần lượt là \({n_1},{n_2},...{n_m}\). |
Bảng tần số ghép nhóm
Để lập bảng tần số ghép nhóm ở dạng bảng ngang, ta có thể làm như sau: Bước 1. Xác định các nhóm của mẫu dữ liệu ghép nhóm và tìm tần số của mỗi nhóm đó. Bước 2. Lập bảng gồm 2 dòng và một số cột. Theo thứ tự từ trên xuống dưới, ta lần lượt ghi: - Cột đầu tiên: Nhóm, Tần số (n) - Các cột tiếp theo lần lượt ghi tên nhóm và tần số của nhóm đó. - Cột cuối cùng: Cộng, N =… |
Chú ý: Bảng tần số ghép nhóm ở dạng bảng dọc được lập bằng cách tương tự như trên.
Ví dụ: Ta có bảng tần số ghép nhóm cho mẫu số liệu chiều cao (đơn vị là cm) của học sinh lớp 9A với các nhóm [155; 158), [158; 161), [161; 164), [164;167) ở dạng bảng ngang:

hoặc ở dạng bảng dọc:
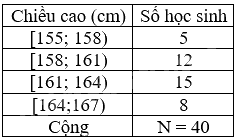
Biểu đồ tần số ghép nhóm
Để vẽ biểu đồ tần số ghép nhóm ở dạng biểu đồ cột của một mẫu số liệu ghép nhóm, ta có thể thực hiện theo các bước sau: Bước 1. Lập bảng tần số ghép nhóm của mẫu số liệu được ghép nhóm đã cho Bước 2. Vẽ biểu đồ cột biểu diễn số liệu thống kê trong bảng tần số ghép nhóm nhận được ở Bước 1 (các cột được ghép sát nhau). |
Ví dụ: Biểu đồ tần số ghép nhóm chiều cao của học sinh lớp 9A:
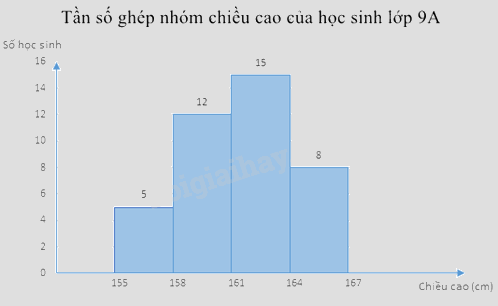
2. Tần số tương đối ghép nhóm, bảng tần số tương đối ghép nhóm, biểu đồ tần số tương đối ghép nhóm
Tần số tương đối ghép nhóm
Tần số tương đối ghép nhóm (hay tần số tương đối) \({f_i}\) của nhóm I là tỉ số giữa tần số \({n_i}\) của nhóm đó và số lượng N các số liệu trong mẫu số liệu thống kê: \({f_i} = \frac{{{n_i}}}{N}\). Ta thường viết tần số tương đối ghép nhóm dưới dạng phần trăm. |
Bảng tần số tương đối ghép nhóm
Để lập bảng tần số tương đối ghép nhóm ở dạng bảng ngang, ta có thể làm như sau: Bước 1. Xác định các nhóm của mẫu dữ liệu ghép nhóm và tìm tần số tương đối của mỗi nhóm đó. Bước 2. Lập bảng gồm 2 dòng và một số cột. Theo thứ tự từ trên xuống dưới, ta lần lượt ghi: - Cột đầu tiên: Nhóm, Tần số tương đối (%) - Các cột tiếp theo lần lượt ghi nhóm và tần số tương đối của nhóm đó. - Cột cuối cùng: Cộng, 100. |
Chú ý: Bảng tần số tương đối ghép nhóm ở dạng bảng dọc được lập bằng cách tương tự như trên.
Ví dụ: Bảng tần số ghép nhóm cho mẫu số liệu chiều cao (đơn vị là cm) của học sinh lớp 9A với các nhóm [155; 158), [158; 161), [161; 164), [164;167):

Từ bảng tần số ghép nhóm trên, ta có:
Tổng số học sinh của lớp \(n = 5 + 12 + 15 + 8 = 40\).
Tỉ số học sinh có chiều cao từ 150 cm đến dưới 158 cm là \(\frac{5}{{40}} = 12,5\% \);
từ 158 cm đến dưới 161 cm là \(\frac{{12}}{{40}} = 30\% \);
từ 161 đến dưới 164 cm là \(\frac{{15}}{{40}} = 37,5\% \);
từ 164 đến dưới 167 cm là \(\frac{8}{{40}} = 20\% \).
Bảng tần số tương đối ghép nhóm cho mẫu số này với các nhóm [155; 158), [158; 161), [161; 164), [164;167) là:

Biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột
Để vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột của một mẫu số liệu ghép nhóm, ta có thể thực hiện theo các bước sau: Bước 1. Lập bảng tần số tương đối ghép nhóm của mẫu số liệu được ghép nhóm đã cho Bước 2. Vẽ biểu đồ cột biểu diễn số liệu thống kê trong bảng tần số ghép nhóm nhận được ở Bước 1. |
Biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ đoạn thẳng
Để vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ đoạn thẳng của một mẫu số liệu ghép nhóm, ta có thể thực hiện các bước sau: Bước 1. Lập bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đã cho Bước 2. Vẽ biểu đồ đoạn thẳng biểu diễn các số liệu thống kê trong bảng tần số tương đối ghép nhóm nhận được ở Bước 1. |
Ví dụ: Bảng tần số tương đối ghép nhóm của mẫu số liệu thống kê số lượng người đến đọc sách trong 100 ngày liên tiếp của một thư viện.

Biểu đồ tần số tương đối ghép nhóm dạng cột của bảng tần số tương đối trên là:
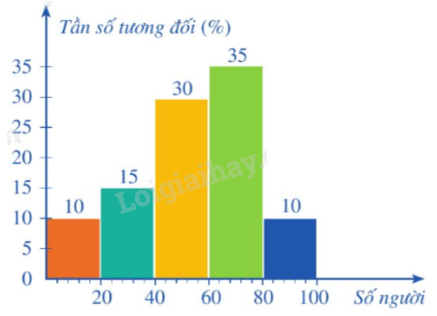
Biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng của bảng tần số tương đối trên là:
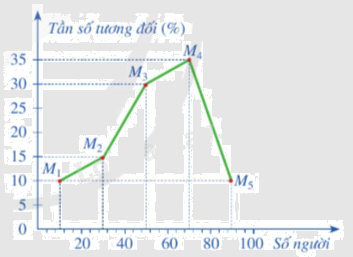
Trong chương trình Toán 9, việc học về thống kê và xử lý dữ liệu đóng vai trò quan trọng trong việc phát triển tư duy logic và khả năng phân tích của học sinh. Một trong những khái niệm cốt lõi của phần này là Tần số ghép nhóm và Tần số tương đối ghép nhóm. Bài viết này sẽ đi sâu vào lý thuyết, công thức và các ví dụ minh họa để giúp bạn hiểu rõ hơn về hai khái niệm này trong chương trình Toán 9 Cánh diều.
Trước khi đi vào lý thuyết về tần số ghép nhóm, chúng ta cần hiểu rõ quy trình thu thập và tổ chức dữ liệu. Dữ liệu có thể được thu thập từ nhiều nguồn khác nhau, như khảo sát, quan sát hoặc các báo cáo thống kê. Sau khi thu thập, dữ liệu thường được tổ chức thành bảng tần số để dễ dàng phân tích.
Tần số ghép nhóm là số lần xuất hiện của một giá trị hoặc một khoảng giá trị trong một tập dữ liệu. Để ghép nhóm dữ liệu, chúng ta thường chia tập dữ liệu thành các khoảng giá trị (gọi là các lớp) và đếm số lượng giá trị thuộc mỗi lớp. Ví dụ:
Tần số tương đối ghép nhóm là tỷ lệ phần trăm của tần số ghép nhóm so với tổng số lượng dữ liệu. Công thức tính tần số tương đối ghép nhóm là:
Tần số tương đối ghép nhóm = (Tần số ghép nhóm / Tổng số lượng dữ liệu) * 100%
Ví dụ, tiếp tục với tập dữ liệu điểm kiểm tra Toán ở trên:
Việc sử dụng tần số ghép nhóm và tần số tương đối ghép nhóm mang lại nhiều lợi ích trong việc phân tích dữ liệu:
Để củng cố kiến thức về tần số ghép nhóm và tần số tương đối ghép nhóm, hãy thử giải các bài tập sau:
Lý thuyết Tần số ghép nhóm và tần số tương đối ghép nhóm là một công cụ quan trọng trong việc phân tích dữ liệu và rút ra những kết luận hữu ích. Việc nắm vững kiến thức này sẽ giúp bạn tự tin hơn trong việc giải quyết các bài toán thực tế và đưa ra các quyết định sáng suốt. Hy vọng bài viết này đã cung cấp cho bạn những thông tin cần thiết và hữu ích về chủ đề này.