Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 76 SGK Toán 9 tập 2 - Cánh diều tại giaitoan.edu.vn. Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập này thuộc chương trình Toán 9 tập 2, tập trung vào việc rèn luyện kỹ năng giải bài toán liên quan đến các kiến thức đã học.
Trong Hình 22, cho biết (widehat {AOC} = a.) Tính số đo của các cung và góc sau theo a. a) (oversetfrown{ADC},widehat{ABC;}) b) (oversetfrown{ADC},widehat{ABC;}) c) (widehat{ADC}+widehat{ABC.})
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 76SGK Toán 9 Cánh diều
Cho đường tròn (O) ngoại tiếp tam giác đều ABC và điểm M thuộc cung nhỏ BC (M khác B và C). Tính số đo góc BMC.
Phương pháp giải:
Bước 1: Tính số đo cung AB và AC.
Bước 2: \(\widehat {BMC} = \frac{1}{2}\)sđ\(\overset\frown{BAC}.\)
Lời giải chi tiết:
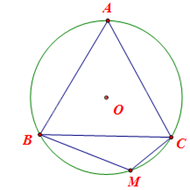
Vì tam giác ABC đều nên \(\widehat {ABC} = \widehat {ACB} = 60^\circ .\) Mà tam giác ABC và nội tiếp (O) nên sđ\(\overset\frown{AB}=2\)\(\widehat {ACB}\), sđ\(\overset\frown{AC}=2\)\(\widehat {ABC}\).
Suy ra sđ\(\overset\frown{AB}=\)sđ\(\overset\frown{AC}=2.60{}^\circ =120{}^\circ .\) Do đó
sđ\(\overset\frown{BAC}=\) sđ\(\overset\frown{AB}+\)sđ\(\overset\frown{AC}=120{}^\circ +120{}^\circ =240{}^\circ .\)
Góc BMC là góc nội tiếp chắn cung BAC của (O) nên \(\widehat {BMC} = \frac{1}{2}\)sđ\(\overset\frown{BAC}=\frac{1}{2}.240{}^\circ =120{}^\circ .\)
Vậy \(\widehat {BMC} = 120^\circ .\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 76 SGK Toán 9 Cánh diều
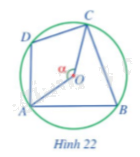
Trong Hình 22, cho biết \(\widehat {AOC} = \alpha.\)
Tính số đo của các cung và góc sau theo \( \alpha\).
a) \(\overset\frown{ADC},\widehat{ABC;}\)
b) \(\overset\frown{ADC},\widehat{ABC;}\)
c) \(\widehat{ADC}+\widehat{ABC.}\)
Phương pháp giải:
Lý thuyết: Trong một đường tròn, số đo góc ở tâm bằng số đo cung bị chắn, số đo góc nội tiếp bằng nửa số đo cung bị chắn.
Lời giải chi tiết:
a) Xét (O) có \(\widehat {AOC}\) là góc ở tâm chắn cung CDA nên \(\widehat {AOC}\)= sđ\(\overset\frown{CDA}= \alpha.\)
\(\widehat {ABC}\) là góc nội tiếp chắn cung CDA của (O) nên \(\widehat {ABC}\)= \(\frac{1}{2}\)sđ\(\overset\frown{CDA}=\frac{ \alpha}{2}.\)
b) Xét (O) có sđ\(\overset\frown{ABC}=360{}^\circ -\)sđ\(\overset\frown{CDA}=360{}^\circ - \alpha.\)
\(\widehat {ADC}\) là góc nội tiếp chắn cung ABC của (O) nên\(\widehat {ADC}\) = \(\frac{1}{2}\)sđ\(\overset\frown{ABC}=\frac{360{}^\circ - \alpha}{2}.\)
c) \(\widehat {ADC} + \widehat {ABC} = \frac{{360^\circ - \alpha}}{2} + \frac{ \alpha}{2} = \frac{{360^\circ - \alpha + \alpha}}{2} = 180^\circ .\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 76 SGK Toán 9 Cánh diều
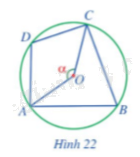
Trong Hình 22, cho biết \(\widehat {AOC} = \alpha.\)
Tính số đo của các cung và góc sau theo \( \alpha\).
a) \(\overset\frown{ADC},\widehat{ABC;}\)
b) \(\overset\frown{ADC},\widehat{ABC;}\)
c) \(\widehat{ADC}+\widehat{ABC.}\)
Phương pháp giải:
Lý thuyết: Trong một đường tròn, số đo góc ở tâm bằng số đo cung bị chắn, số đo góc nội tiếp bằng nửa số đo cung bị chắn.
Lời giải chi tiết:
a) Xét (O) có \(\widehat {AOC}\) là góc ở tâm chắn cung CDA nên \(\widehat {AOC}\)= sđ\(\overset\frown{CDA}= \alpha.\)
\(\widehat {ABC}\) là góc nội tiếp chắn cung CDA của (O) nên \(\widehat {ABC}\)= \(\frac{1}{2}\)sđ\(\overset\frown{CDA}=\frac{ \alpha}{2}.\)
b) Xét (O) có sđ\(\overset\frown{ABC}=360{}^\circ -\)sđ\(\overset\frown{CDA}=360{}^\circ - \alpha.\)
\(\widehat {ADC}\) là góc nội tiếp chắn cung ABC của (O) nên\(\widehat {ADC}\) = \(\frac{1}{2}\)sđ\(\overset\frown{ABC}=\frac{360{}^\circ - \alpha}{2}.\)
c) \(\widehat {ADC} + \widehat {ABC} = \frac{{360^\circ - \alpha}}{2} + \frac{ \alpha}{2} = \frac{{360^\circ - \alpha + \alpha}}{2} = 180^\circ .\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 76SGK Toán 9 Cánh diều
Cho đường tròn (O) ngoại tiếp tam giác đều ABC và điểm M thuộc cung nhỏ BC (M khác B và C). Tính số đo góc BMC.
Phương pháp giải:
Bước 1: Tính số đo cung AB và AC.
Bước 2: \(\widehat {BMC} = \frac{1}{2}\)sđ\(\overset\frown{BAC}.\)
Lời giải chi tiết:
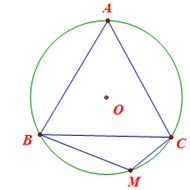
Vì tam giác ABC đều nên \(\widehat {ABC} = \widehat {ACB} = 60^\circ .\) Mà tam giác ABC và nội tiếp (O) nên sđ\(\overset\frown{AB}=2\)\(\widehat {ACB}\), sđ\(\overset\frown{AC}=2\)\(\widehat {ABC}\).
Suy ra sđ\(\overset\frown{AB}=\)sđ\(\overset\frown{AC}=2.60{}^\circ =120{}^\circ .\) Do đó
sđ\(\overset\frown{BAC}=\) sđ\(\overset\frown{AB}+\)sđ\(\overset\frown{AC}=120{}^\circ +120{}^\circ =240{}^\circ .\)
Góc BMC là góc nội tiếp chắn cung BAC của (O) nên \(\widehat {BMC} = \frac{1}{2}\)sđ\(\overset\frown{BAC}=\frac{1}{2}.240{}^\circ =120{}^\circ .\)
Vậy \(\widehat {BMC} = 120^\circ .\)
Mục 2 trang 76 SGK Toán 9 tập 2 - Cánh diều thường bao gồm các bài tập vận dụng kiến thức về hàm số bậc hai, đồ thị hàm số bậc hai, và các ứng dụng của hàm số bậc hai trong thực tế. Để giải quyết các bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản, công thức tính toán, và phương pháp vẽ đồ thị hàm số.
Mục 2 thường bao gồm các dạng bài tập sau:
Dưới đây là hướng dẫn giải chi tiết từng bài tập trong Mục 2 trang 76 SGK Toán 9 tập 2 - Cánh diều:
...
...
...
Ví dụ: Cho hàm số y = x2 - 4x + 3. Hãy tìm tọa độ đỉnh của parabol.
Giải:
Hệ số a = 1, b = -4, c = 3.
Hoành độ đỉnh: x = -b/2a = -(-4)/(2*1) = 2.
Tung độ đỉnh: y = 22 - 4*2 + 3 = -1.
Vậy tọa độ đỉnh của parabol là (2; -1).
Việc giải bài tập Mục 2 trang 76 SGK Toán 9 tập 2 - Cánh diều đòi hỏi sự nắm vững kiến thức và kỹ năng vận dụng linh hoạt. Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt nhất.
| Công thức | Mô tả |
|---|---|
| x = -b/2a | Hoành độ đỉnh của parabol |
| Δ = b2 - 4ac | Biệt thức của phương trình bậc hai |
| x1,2 = (-b ± √Δ) / 2a | Nghiệm của phương trình bậc hai |