Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 6 trang 79 sách giáo khoa Toán 9 tập 2 - Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để bạn có thể hiểu rõ bản chất của bài toán.
Khung thép của một phần sân khấu có dạng đường tròn bán kính 15m. Mắt của một người thợ ở vị trí A nhìn hai đèn ở các vị trí B, C (A, B, C cùng thuộc đường tròn bán kính 15m), bằng cách nào đó, người thợ thấy rằng góc nhìn (widehat {BAC} = 30^circ ) (hình 31). Khoảng cách giữa hai vị trí B và C bằng bao nhiêu mét?
Đề bài
Khung thép của một phần sân khấu có dạng đường tròn bán kính 15m. Mắt của một người thợ ở vị trí A nhìn hai đèn ở các vị trí B, C (A, B, C cùng thuộc đường tròn bán kính 15m), bằng cách nào đó, người thợ thấy rằng góc nhìn \(\widehat {BAC} = 30^\circ \) (hình 31). Khoảng cách giữa hai vị trí B và C bằng bao nhiêu mét?

Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Bước 1: Tính số đo góc BOC.
Bước 2: Chứng minh tam giác BOC đều.
Bước 3: Tính BC (= R)
Lời giải chi tiết
Bài toán được mô tả bằng hình vẽ sau:
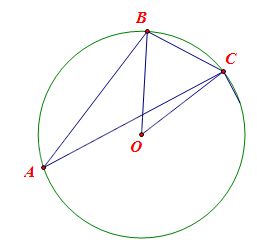
Trong đó: \(\widehat {BAC} = 30^\circ ,BO = OC = R = 15m.\)
Xét (O): góc BAC là góc nội tiếp chắn cung BC nên \(\widehat{BAC}=\frac{1}{2}sđ\overset\frown{BC}=30{}^\circ \) do đó \(sđ\overset\frown{BC}=60{}^\circ \).
Góc BOC là góc ở tâm chắc cung BC của (O) nên \(\widehat{BOC}=sđ\overset\frown{BC}=60{}^\circ \).
Xét tam giác BOC có:
BO = CO (= R)
\(\widehat {BOC} = 60^\circ \)
Nên tam giác BOC đều
suy ra BO = CO = BC = 15m.
Vậy khoảng cách giữa B và C là 15m.
Bài tập 6 trang 79 SGK Toán 9 tập 2 - Cánh diều thuộc chương trình học về hàm số bậc hai. Bài tập này yêu cầu học sinh vận dụng kiến thức về định nghĩa hàm số, tập xác định, tập giá trị, và cách vẽ đồ thị hàm số bậc hai để giải quyết các vấn đề cụ thể.
Bài tập 6 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh:
Để giải bài tập 6 trang 79 SGK Toán 9 tập 2 - Cánh diều một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
Câu a: Cho hàm số y = 2x2 - 5x + 3. Hãy xác định hệ số a, b, c.
Lời giải:
Hàm số y = 2x2 - 5x + 3 có:
Câu b: Tìm tọa độ đỉnh của parabol.
Lời giải:
Tọa độ đỉnh của parabol là (x0, y0), trong đó:
Vậy tọa độ đỉnh của parabol là (5/4, -1/8).
Câu c: Xác định trục đối xứng của parabol.
Lời giải:
Trục đối xứng của parabol là đường thẳng x = x0 = 5/4.
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác.
Bài tập 6 trang 79 SGK Toán 9 tập 2 - Cánh diều là một bài tập quan trọng giúp bạn hiểu rõ hơn về hàm số bậc hai. Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả mà chúng tôi cung cấp, bạn sẽ tự tin giải quyết bài tập này một cách dễ dàng.