Chào mừng các em học sinh đến với lời giải chi tiết bài tập 5 trang 124 SGK Toán 9 tập 1 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập 5 thuộc chương trình học Toán 9 tập 1, tập trung vào việc vận dụng các kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế.
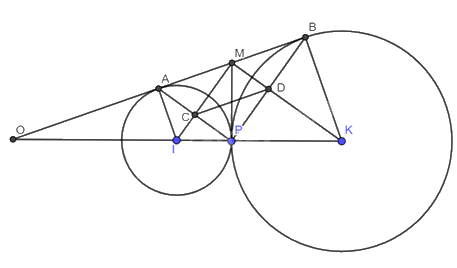
Cho hai đường tròn (left( {I;r} right)) và (left( {K;R} right)) tiếp xúc ngoài với nhau tại (P) với (R ne r), đường thẳng (a) lần lượt tiếp xúc với (left( {I;r} right)) và (left( {K;R} right)) tại (A) và (B,a) cắt (KI) tại (O). Đường thẳng qua (P) vuông góc với (IK) cắt đường thẳng (a) tại (M). Chứng minh: a) (frac{{OI}}{{OK}} = frac{r}{R}); b) (AB = 2MP); c) (widehat {IMK} = 90^circ ).
Đề bài
Cho hai đường tròn \(\left( {I;r} \right)\) và \(\left( {K;R} \right)\) tiếp xúc ngoài với nhau tại \(P\) với \(R \ne r\), đường thẳng \(a\) lần lượt tiếp xúc với \(\left( {I;r} \right)\) và \(\left( {K;R} \right)\) tại \(A\) và \(B,a\) cắt \(KI\) tại \(O\). Đường thẳng qua \(P\) vuông góc với \(IK\) cắt đường thẳng \(a\) tại \(M\). Chứng minh:
a) \(\frac{{OI}}{{OK}} = \frac{r}{R}\);
b) \(AB = 2MP\);
c) \(\widehat {IMK} = 90^\circ \).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào kiến thức đã học để chứng minh.
Lời giải chi tiết
a) Do \(AI\) là tiếp tuyến của \(\left( I \right)\) nên \(AI \bot AB\)
Do \(BK\) là tiếp tuyến của \(\left( K \right)\) nên \(KB \bot AB\)
Từ đó suy ra \(AI//BK\)
Xét tam giác \(OBK\) có: \(AI//BK \Rightarrow \frac{{OI}}{{OK}} = \frac{{AI}}{{BK}} = \frac{r}{R}\) (định lí Thalet).
b) Xét \(\left( I \right)\) có \(MP,MA\) là hai tiếp tuyến cắt nhau
\( \Rightarrow MP = MA\)(1).
Xét \(\left( K \right)\) có \(MP,MB\) là hai tiếp tuyến cắt nhau
\( \Rightarrow MP = MB\)(2).
Từ (1) và (2) suy ra \(MP + MP = MA + MB \Rightarrow 2MP = AB\)
c) Do \(AI//BK \Rightarrow \widehat {OIA} = \widehat {IKB}\) (2 góc đồng vị).
Mà \(\widehat {AIK} + \widehat {OAI} = 180^\circ \) (2 góc kề bù) nên \(\widehat {AIK} + \widehat {IKB} = 180^\circ \) (3).
Do \(MP,MA\) là hai tiếp tuyến cắt nhau
\( \Rightarrow IM\) là phân giác \(\widehat {AIP} \Rightarrow \widehat {MIP} = \frac{1}{2}\widehat {AIP}\) (4).
Do \(MP,MB\) là hai tiếp tuyến cắt nhau
\( \Rightarrow KM\) là phân giác \(\widehat {IKP} \Rightarrow \widehat {MKP} = \frac{1}{2}\widehat {IKP}\) (5).
Từ (3), (4) và (5) suy ra \(\frac{1}{2}\widehat {AIP} + \frac{1}{2}\widehat {IKP} = \frac{1}{2}.180^\circ \Rightarrow \widehat {MIP} + \widehat {MKP} = 90^\circ \)
Xét tam giác \(IMK\) có: \(\widehat {MIP} + \widehat {MKP} = 90^\circ \Rightarrow \widehat {IMK} = 90^\circ \)
Bài tập 5 trang 124 SGK Toán 9 tập 1 - Cánh diều yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán liên quan đến đồ thị hàm số và ứng dụng thực tế. Dưới đây là hướng dẫn chi tiết từng bước để giải quyết bài tập này:
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức cơ bản:
Đề bài: (Giả sử đề bài cụ thể của bài 5a ở đây)
Lời giải:
Đề bài: (Giả sử đề bài cụ thể của bài 5b ở đây)
Lời giải:
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự sau:
Khi giải các bài tập về hàm số, các em cần lưu ý:
Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin hơn khi giải bài tập 5 trang 124 SGK Toán 9 tập 1 - Cánh diều. Chúc các em học tập tốt!
| Tiêu chí | Mô tả |
|---|---|
| Hàm số bậc nhất | y = ax + b (a ≠ 0) |
| Hàm số bậc hai | y = ax2 + bx + c (a ≠ 0) |
| Bảng tóm tắt các công thức quan trọng | |