Chào mừng các em học sinh đến với lời giải chi tiết bài tập 9 trang 125 SGK Toán 9 tập 1 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập hiệu quả, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Bài tập 9 thuộc chương trình học Toán 9 tập 1, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Chúng tôi sẽ hướng dẫn các em từng bước để hiểu rõ bản chất của bài toán và cách tiếp cận phù hợp.
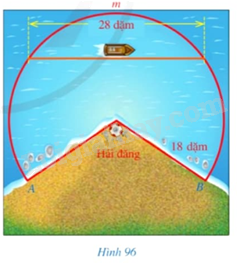
Hình 96 biểu diễn vùng biển được chiếu sáng bởi một hải đăng có dạng một hình quạt tròn với bán kính 18 dặm, cung (AmB) có số đo (245^circ ). a) Hãy tính diện tích vùng biển có thể nhìn thấy ánh sáng từ hải đăng theo đơn vị kilomét vuông (lấy 1 dặm = 1600m, (pi = 3,14) và làm tròn kết quả đến hàng đơn vị). b) Giả sử một con thuyền di chuyển dọc theo dây cung có độ dài 28 dặm của đường tròn với tâm là tâm của hình quạt tròn, bán kính 18 dặm. Tính khoảng cách nhỏ nhất từ con thuyền đến
Đề bài
Hình 96 biểu diễn vùng biển được chiếu sáng bởi một hải đăng có dạng một hình quạt tròn với bán kính 18 dặm, cung \(AmB\) có số đo \(245^\circ \).
a) Hãy tính diện tích vùng biển có thể nhìn thấy ánh sáng từ hải đăng theo đơn vị kilomét vuông (lấy 1 dặm = 1609m, \(\pi = 3,14\) và làm tròn kết quả đến hàng đơn vị).
b) Giả sử một con thuyền di chuyển dọc theo dây cung có độ dài 28 dặm của đường tròn với tâm là tâm của hình quạt tròn, bán kính 18 dặm. Tính khoảng cách nhỏ nhất từ con thuyền đến hải đăng (theo đơn vị dặm và làm tròn kết quả đến hàng đơn vị).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào kiến thức đã học để chứng minh.
Lời giải chi tiết
a) Đổi 1 dặm = 1609m = 1,609km
suy ra 18 dặm = 18.1,609 (km)
Diện tích vùng biển có thể nhìn thấy ánh sáng từ hải đăng là:
\(S = \frac{{\pi .{R^2}.n}}{{360}} = \frac{{\pi .{{\left( {18.1,609} \right)}^2}.245}}{{360}} \approx 1793\left( {km^2} \right)\).
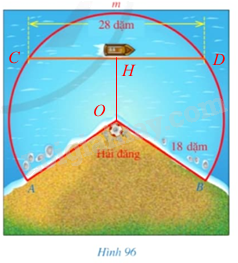
b) Kẻ \(OH \bot CD\)
Xét (O) có \(OH \bot CD\) nên H là trung điểm của CD.
Suy ra \(CH = \frac{1}{2} CD = 14\) (dặm)
Xét tam giác OHC vuông tại H có:
\(OC^2 =OH^2+HC^2\)
suy ra \(OH^2=18^2 - 14^2 = 128\)
suy ra \(OH \approx 11\) (dặm)
Vậy khoảng cách nhỏ nhất từ con thuyền đến hải đăng là khoảng 11 dặm.
Bài tập 9 trang 125 SGK Toán 9 tập 1 - Cánh diều yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết một bài toán thực tế. Để giải bài tập này, chúng ta cần xác định được các yếu tố quan trọng như hệ số góc, tung độ gốc, và các điểm thuộc đồ thị hàm số.
Trước khi bắt đầu giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài tập 9, đề bài thường yêu cầu chúng ta tìm phương trình đường thẳng hoặc parabol đi qua các điểm cho trước, hoặc xác định giao điểm của hai đường thẳng hoặc parabol.
Để giải bài tập 9, chúng ta có thể sử dụng các phương pháp sau:
(Ở đây sẽ là lời giải chi tiết cho bài tập 9, bao gồm các bước giải, giải thích rõ ràng và các ví dụ minh họa. Lời giải sẽ được trình bày chi tiết, dễ hiểu, phù hợp với trình độ của học sinh lớp 9.)
Để giúp các em hiểu rõ hơn về phương pháp giải bài tập 9, chúng ta sẽ xem xét một ví dụ minh họa sau:
(Ví dụ minh họa sẽ được trình bày chi tiết, bao gồm đề bài, lời giải và giải thích.)
Để củng cố kiến thức và kỹ năng giải bài tập 9, các em có thể luyện tập thêm với các bài tập tương tự sau:
Bài tập 9 trang 125 SGK Toán 9 tập 1 - Cánh diều là một bài tập quan trọng giúp các em củng cố kiến thức về hàm số bậc nhất và hàm số bậc hai. Hy vọng rằng với hướng dẫn chi tiết và ví dụ minh họa trên, các em sẽ tự tin hơn trong việc giải quyết các bài tập tương tự.
Để hiểu rõ hơn về bài tập 9, các em có thể tham khảo thêm các kiến thức sau:
Các em có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:
Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!