Định lí Viète là một trong những kiến thức quan trọng trong chương trình Toán 9, đặc biệt là sách Cánh diều. Nắm vững lý thuyết này giúp học sinh giải quyết các bài toán liên quan đến phương trình bậc hai một cách nhanh chóng và hiệu quả.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu cùng với các bài tập thực hành đa dạng để bạn có thể nắm vững kiến thức và tự tin làm bài.
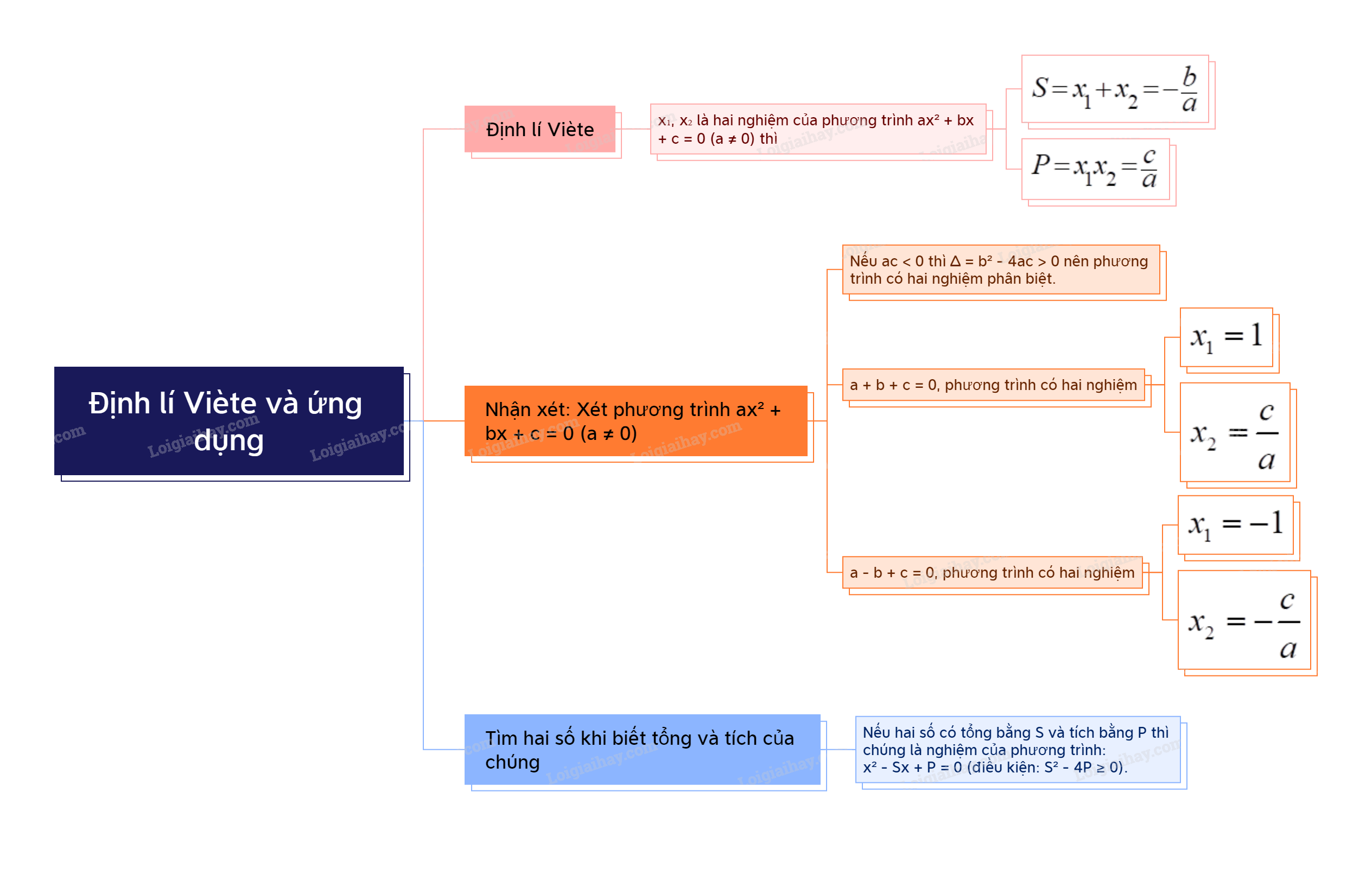
1. Định lí Viète Nếu \({x_1},{x_2}\) là hai nghiệm của phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) thì \({x_1} + {x_2} = - \frac{b}{a}\); \({x_1}{x_2} = \frac{c}{a}.\)
1. Định lí Viète
Nếu \({x_1},{x_2}\) là hai nghiệm của phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) thì \({x_1} + {x_2} = - \frac{b}{a}\); \({x_1}{x_2} = \frac{c}{a}.\) |
Ví dụ: Phương trình \(2{x^2} + 11x + 7 = 0\) có: \(\Delta = {11^2} - 4.2.7 = 65 > 0\) nên phương trình có hai nghiệm phân biệt \({x_1},{x_2}\).
Theo định lí Viète, ta có: \({x_1} + {x_2} = - \frac{{11}}{2};{x_1}{x_2} = \frac{7}{2}\).
Nhận xét:
Xét phương trình \(a{x^2} + bx + c = 0\) \(\left( {a \ne 0} \right)\): - Nếu \(ac < 0\) thì \(\Delta = {b^2} - 4ac > 0\), do đó phương trình luôn có hai nghiệm phân biệt. - Nếu \(a + b + c = 0\) thì phương trình có một nghiệm là \({x_1} = 1\), còn nghiệm kia là \({x_2} = \frac{c}{a}\). - Nếu \(a - b + c = 0\) thì phương trình có nghiệm là \({x_1} = - 1\), còn nghiệm kia là \({x_2} = - \frac{c}{a}\). |
Ví dụ: Phương trình \({x^2} + 3572x - 3573 = 0\) có \(a = 1 > 0,c = - 3573 < 0\), suy ra a và c trái dấu. Do đó phương trình có hai nghiệm phân biệt.
Phương trình \({x^2} - 6x + 5 = 0\) có \(a + b + c = 1 + \left( { - 6} \right) + 5 = 0\) nên phương trình có hai nghiệm: \({x_1} = 1,{x_2} = 5\).
Phương trình \(5{x^2} + 14x + 9 = 0\) có \(a - b + c = 5 - 14 + 9 = 0\) nên phương trình có hai nghiệm: \({x_1} = - 1,{x_2} = - \frac{9}{5}\).
2. Tìm hai số khi biết tổng và tích
Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là hai nghiệm của phương trình bậc hai: \({x^2} - Sx + P = 0\). Điều kiện để có hai số đó là \({S^2} - 4P \ge 0\). |
Ví dụ: Hai số có tổng bằng 9, tích bằng 20 là nghiệm của phương trình \({x^2} + 9x + 20 = 0\).
Ta có: \(\Delta = {\left( { - 9} \right)^2} - 4.1.20 = 1,\sqrt \Delta = 1\).
Suy ra phương trình có hai nghiệm \({x_1} = \frac{{9 - 1}}{2} = 4;{x_2} = \frac{{9 + 1}}{2} = 5\).
Vậy hai số cần tìm là 4 và 5.
Định lí Viète là một công cụ mạnh mẽ trong việc giải quyết các bài toán liên quan đến phương trình bậc hai. Trong chương trình Toán 9 Cánh diều, định lí này được trình bày một cách rõ ràng và có nhiều ứng dụng thực tế. Bài viết này sẽ cung cấp một cái nhìn tổng quan về lý thuyết Định lí Viète và các ứng dụng quan trọng của nó.
Cho phương trình bậc hai ax2 + bx + c = 0 (với a ≠ 0). Nếu phương trình có hai nghiệm x1 và x2 thì:
x1 + x2 = -b/ax1.x2 = c/aĐây là hai công thức cơ bản mà học sinh cần nắm vững để áp dụng Định lí Viète vào giải toán.
Định lí Viète có rất nhiều ứng dụng trong việc giải toán, đặc biệt là trong các bài toán sau:
x1 + x2 > 0 và x1.x2 > 0 thì hai nghiệm đều dương.Ví dụ 1: Cho phương trình x2 - 5x + 6 = 0. Hãy tìm tổng và tích của hai nghiệm.
Giải:
Ta có a = 1, b = -5, c = 6. Theo Định lí Viète:
x1 + x2 = -(-5)/1 = 5x1.x2 = 6/1 = 6Ví dụ 2: Cho phương trình 2x2 + 3x - 5 = 0. Hãy xác định dấu của hai nghiệm.
Giải:
Ta có a = 2, b = 3, c = -5. Theo Định lí Viète:
x1 + x2 = -3/2 < 0x1.x2 = -5/2 < 0Vì tổng và tích hai nghiệm đều âm nên hai nghiệm có dấu trái nhau.
Định lí Viète không chỉ áp dụng cho phương trình bậc hai mà còn mở rộng cho phương trình bậc ba. Cho phương trình bậc ba ax3 + bx2 + cx + d = 0 (với a ≠ 0) có ba nghiệm x1, x2 và x3 thì:
x1 + x2 + x3 = -b/ax1.x2 + x1.x3 + x2.x3 = c/ax1.x2.x3 = -d/aĐể nắm vững lý thuyết Định lí Viète và ứng dụng của nó, bạn nên luyện tập thường xuyên với các bài tập khác nhau. Tại giaitoan.edu.vn, chúng tôi cung cấp một hệ thống bài tập đa dạng, từ cơ bản đến nâng cao, giúp bạn củng cố kiến thức và nâng cao kỹ năng giải toán.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về Lý thuyết Định lí Viète và ứng dụng Toán 9 Cánh diều. Chúc bạn học tập tốt!