Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 2 trang 79 sách giáo khoa Toán 9 tập 2 - Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp các em học sinh nắm vững kiến thức và đạt kết quả cao trong môn Toán.
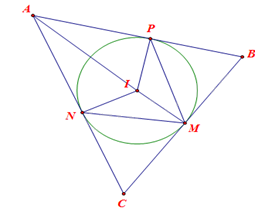
Cho đường tròn (I) nội tiếp tam giác ABC và lần lượt tiếp xúc với các cạnh BC, CA, AB tại M, N, P. Chứng minh (widehat {AIN} = widehat {PMN} = frac{1}{2}widehat {PIN.})
Đề bài
Cho đường tròn (I) nội tiếp tam giác ABC và lần lượt tiếp xúc với các cạnh BC, CA, AB tại M, N, P. Chứng minh \(\widehat {AIN} = \widehat {PMN} = \frac{1}{2}\widehat {PIN.}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Bước 1: Lý thuyết: Góc ở tâm bằng số đo cung bị chắn, góc nội tiếp bằng một nửa số đo cung bị chắn, suy ra \(\widehat {PMN} = \frac{1}{2}\widehat {PIN.}\)
Bước 2: Sử dụng tính chất 2 tiếp tuyến cắt nhau để suy ra \(\widehat {AIN} = \frac{1}{2}\widehat {PIN.}\)
Lời giải chi tiết
Xét (I) có:
\(\widehat {PIN}\) là góc ở tâm chắc cung NP nên \(\widehat {PIN}\)= sđ\(\overset\frown{NP}\).
\(\widehat {PMN}\) là góc nội tiếp chắc cung NP nên \(\widehat {PMN}\) = \(\frac{1}{2}\)sđ\(\overset\frown{NP}\).
Suy ra \(\widehat {PMN} = \frac{1}{2}\widehat {PIN.}\)(1)
Ta lại có: \(IN \bot AC,IP \bot AB\) nên AB, AC là 2 tiếp tuyến của (I) nên IA là tia phân giác của góc PIN, hay \(\widehat {AIN} = \frac{1}{2}\widehat {PIN.}\)(2)
Từ (1) và (2) ta có \(\widehat {AIN} = \widehat {PMN} = \frac{1}{2}\widehat {PIN.}\)
Bài tập 2 trang 79 SGK Toán 9 tập 2 - Cánh diều thuộc chương trình học về hàm số bậc hai. Để giải bài tập này, học sinh cần nắm vững kiến thức về:
Bài tập 2 yêu cầu học sinh xác định hệ số a, b, c của các hàm số bậc hai cho trước. Đây là bước quan trọng để phân tích và vẽ đồ thị của hàm số.
Chúng ta sẽ cùng nhau giải từng câu hỏi của bài tập 2:
Trong hàm số y = 2x2 - 5x + 1, ta có:
Trong hàm số y = -x2 + 3x, ta có:
Trong hàm số y = x2 - 7, ta có:
Sau khi xác định được hệ số a, b, c, chúng ta có thể suy ra nhiều thông tin quan trọng về hàm số bậc hai:
Để củng cố kiến thức, bạn có thể tự giải các bài tập sau:
Bài tập 2 trang 79 SGK Toán 9 tập 2 - Cánh diều là một bài tập cơ bản nhưng quan trọng trong việc học về hàm số bậc hai. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ giúp bạn tự tin hơn trong các bài kiểm tra và bài thi.
Giaitoan.edu.vn hy vọng rằng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn giải bài tập một cách hiệu quả. Chúc bạn học tập tốt!