Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 118 và 119 sách giáo khoa Toán 9 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
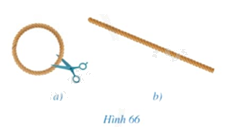
Lấy một vòng tròn (Hình 66a), cắt vòng dây và kéo thẳng vòng dây đó để nhận được sợi dây như ở Hình 66b. Đo chiều dài sợi dây đó.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 118 SGK Toán 9 Cánh diều
Tính chu vi của đường tròn bán kính 5 cm (theo đơn vị centimét và làm tròn kết quả đến hàng phần mười).
Phương pháp giải:
Dựa vào công thức tính chu vi đường tròn: \(C = 2\pi R\) để tính.
Lời giải chi tiết:
Chu vi của đường tròn là:
\(C = 2\pi R = 2\pi .5 = 10\pi \approx 31,4\left( {cm} \right)\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 119 SGK Toán 9 Cánh diều
a) Đánh dấu hai điểm \(A,B\) trên một vòng dây không dãn có dạng đường tròn (Hình 67a), cắt cung \(AB\) của vòng dây và kéo thẳng cung đó để nhận được sợi dây như ở Hình 67b. Đo chiều dài sợi dây đó.
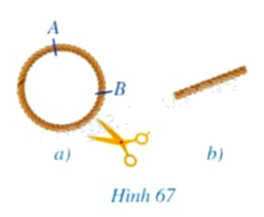
b) Ta coi mỗi đường tròn bán kính \(R\) là một cung tròn có số đo \(360^\circ \). Chia đường tròn đó thành 360 phần bằng nhau, mỗi phần là cung tròn có số đo bằng \(1^\circ \); chu vi của đường tròn khi đó cũng được chia thành \(360\) phần bằng nhau. Tính theo \(R\):
+ Độ dài cung tròn có số đo \(1^\circ \);
+ Độ dài cung tròn có số đo \(n^\circ \).
Phương pháp giải:
Dựa vào kiến thức vừa học để tính.
Lời giải chi tiết:
a) Chiều dài sợi dây \(AB\) là: 5cm.
b) Độ dài cung tròn có số đo \(1^\circ \) là:
\(l = \frac{{2\pi R}}{{360}} = \frac{{\pi R}}{{180}}\).
Độ dài cung tròn có số đo \(n^\circ \) là:
\(l = \frac{{2\pi Rn}}{{360}} = \frac{{\pi Rn}}{{180}}\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 119 SGK Toán 9 Cánh diều
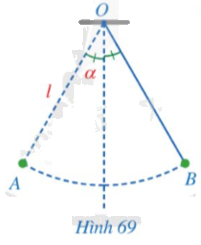
Một con lắc di chuyển từ vị trí \(A\) đến vị trí \(B\) (Hình 69). Tính độ dài quãng đường \(AB\) mà con lắc đó di chuyển, biết rằng sợi dây \(OA\) có độ dài bằng \(l\) và tia \(OA\) tạo với phương thẳng đứng góc \(\alpha \).
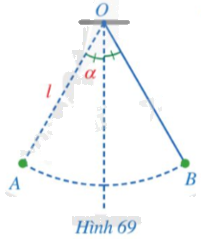
Phương pháp giải:
Dựa vào công thức tính độ dài cung tròn \(l = \frac{{\pi Rn}}{{180}}\) để tính.
Lời giải chi tiết:
Độ dài quãng đường \(AB\) mà con lắc đó di chuyển là:
\(AB = \frac{{\pi .l.2\alpha }}{{180}} = \frac{{\pi l\alpha }}{{90}}.\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 118 SGK Toán 9 Cánh diều
Lấy một vòng tròn (Hình 66a), cắt vòng dây và kéo thẳng vòng dây đó để nhận được sợi dây như ở Hình 66b. Đo chiều dài sợi dây đó.
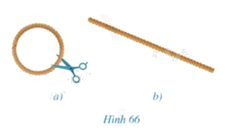
Phương pháp giải:
Dùng thước kẻ để đo độ dài.
Lời giải chi tiết:
HS tự thực hiện theo yêu cầu.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 118 SGK Toán 9 Cánh diều
Tính chu vi của đường tròn bán kính 5 cm (theo đơn vị centimét và làm tròn kết quả đến hàng phần mười).
Phương pháp giải:
Dựa vào công thức tính chu vi đường tròn: \(C = 2\pi R\) để tính.
Lời giải chi tiết:
Chu vi của đường tròn là:
\(C = 2\pi R = 2\pi .5 = 10\pi \approx 31,4\left( {cm} \right)\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 119 SGK Toán 9 Cánh diều
a) Đánh dấu hai điểm \(A,B\) trên một vòng dây không dãn có dạng đường tròn (Hình 67a), cắt cung \(AB\) của vòng dây và kéo thẳng cung đó để nhận được sợi dây như ở Hình 67b. Đo chiều dài sợi dây đó.
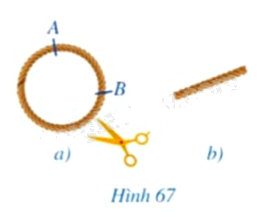
b) Ta coi mỗi đường tròn bán kính \(R\) là một cung tròn có số đo \(360^\circ \). Chia đường tròn đó thành 360 phần bằng nhau, mỗi phần là cung tròn có số đo bằng \(1^\circ \); chu vi của đường tròn khi đó cũng được chia thành \(360\) phần bằng nhau. Tính theo \(R\):
+ Độ dài cung tròn có số đo \(1^\circ \);
+ Độ dài cung tròn có số đo \(n^\circ \).
Phương pháp giải:
Dựa vào kiến thức vừa học để tính.
Lời giải chi tiết:
a) Chiều dài sợi dây \(AB\) là: 5cm.
b) Độ dài cung tròn có số đo \(1^\circ \) là:
\(l = \frac{{2\pi R}}{{360}} = \frac{{\pi R}}{{180}}\).
Độ dài cung tròn có số đo \(n^\circ \) là:
\(l = \frac{{2\pi Rn}}{{360}} = \frac{{\pi Rn}}{{180}}\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 119 SGK Toán 9 Cánh diều
Một con lắc di chuyển từ vị trí \(A\) đến vị trí \(B\) (Hình 69). Tính độ dài quãng đường \(AB\) mà con lắc đó di chuyển, biết rằng sợi dây \(OA\) có độ dài bằng \(l\) và tia \(OA\) tạo với phương thẳng đứng góc \(\alpha \).
Phương pháp giải:
Dựa vào công thức tính độ dài cung tròn \(l = \frac{{\pi Rn}}{{180}}\) để tính.
Lời giải chi tiết:
Độ dài quãng đường \(AB\) mà con lắc đó di chuyển là:
\(AB = \frac{{\pi .l.2\alpha }}{{180}} = \frac{{\pi l\alpha }}{{90}}.\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 118 SGK Toán 9 Cánh diều
Lấy một vòng tròn (Hình 66a), cắt vòng dây và kéo thẳng vòng dây đó để nhận được sợi dây như ở Hình 66b. Đo chiều dài sợi dây đó.
Phương pháp giải:
Dùng thước kẻ để đo độ dài.
Lời giải chi tiết:
HS tự thực hiện theo yêu cầu.
Mục 1 của chương trình Toán 9 tập 1 - Cánh diều tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc nhất. Các bài tập trang 118 và 119 SGK Toán 9 tập 1 - Cánh diều yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, liên quan đến việc xác định hàm số, vẽ đồ thị hàm số và ứng dụng hàm số vào các bài toán hình học.
Bài 1 yêu cầu học sinh nhắc lại các khái niệm cơ bản về hàm số bậc nhất, bao gồm định nghĩa, dạng tổng quát, hệ số góc và giao điểm với các trục tọa độ. Để làm tốt bài này, học sinh cần nắm vững các kiến thức đã học trong các bài trước.
Bài 2 tập trung vào việc xác định hàm số bậc nhất khi biết các yếu tố như hệ số góc và điểm thuộc đồ thị. Học sinh cần sử dụng công thức y = ax + b để tìm ra các hệ số a và b.
Bài 3 yêu cầu học sinh vẽ đồ thị hàm số bậc nhất dựa vào các điểm thuộc đồ thị. Học sinh cần chọn các điểm thích hợp và nối chúng lại để tạo thành đồ thị.
Bài 4 là bài tập vận dụng, yêu cầu học sinh sử dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán hình học. Ví dụ, tìm phương trình đường thẳng đi qua hai điểm cho trước.
Để giúp các em hiểu rõ hơn về cách giải các bài tập trong mục 1 trang 118, 119 SGK Toán 9 tập 1 - Cánh diều, chúng tôi sẽ cung cấp hướng dẫn giải chi tiết cho từng bài tập:
Ví dụ minh họa:
Cho hàm số y = 2x - 1. Hãy xác định hệ số góc và vẽ đồ thị hàm số.
Giải:
Hệ số góc của hàm số là a = 2.
Để vẽ đồ thị hàm số, ta chọn hai điểm thuộc đồ thị, ví dụ: A(0; -1) và B(1; 1). Vẽ hệ trục tọa độ và đánh dấu hai điểm A và B. Nối hai điểm A và B lại để tạo thành đồ thị hàm số.
Khi giải các bài tập về hàm số bậc nhất, học sinh cần lưu ý những điều sau:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 1 trang 118, 119 SGK Toán 9 tập 1 - Cánh diều. Chúc các em học tập tốt!