Bài học này cung cấp đầy đủ lý thuyết về góc ở tâm và góc nội tiếp, một trong những kiến thức quan trọng của chương trình Toán 9 Cánh diều. Chúng tôi sẽ trình bày một cách dễ hiểu, kèm theo các ví dụ minh họa cụ thể.
Giaitoan.edu.vn cam kết mang đến cho bạn trải nghiệm học toán online hiệu quả, giúp bạn tự tin chinh phục các bài toán khó.
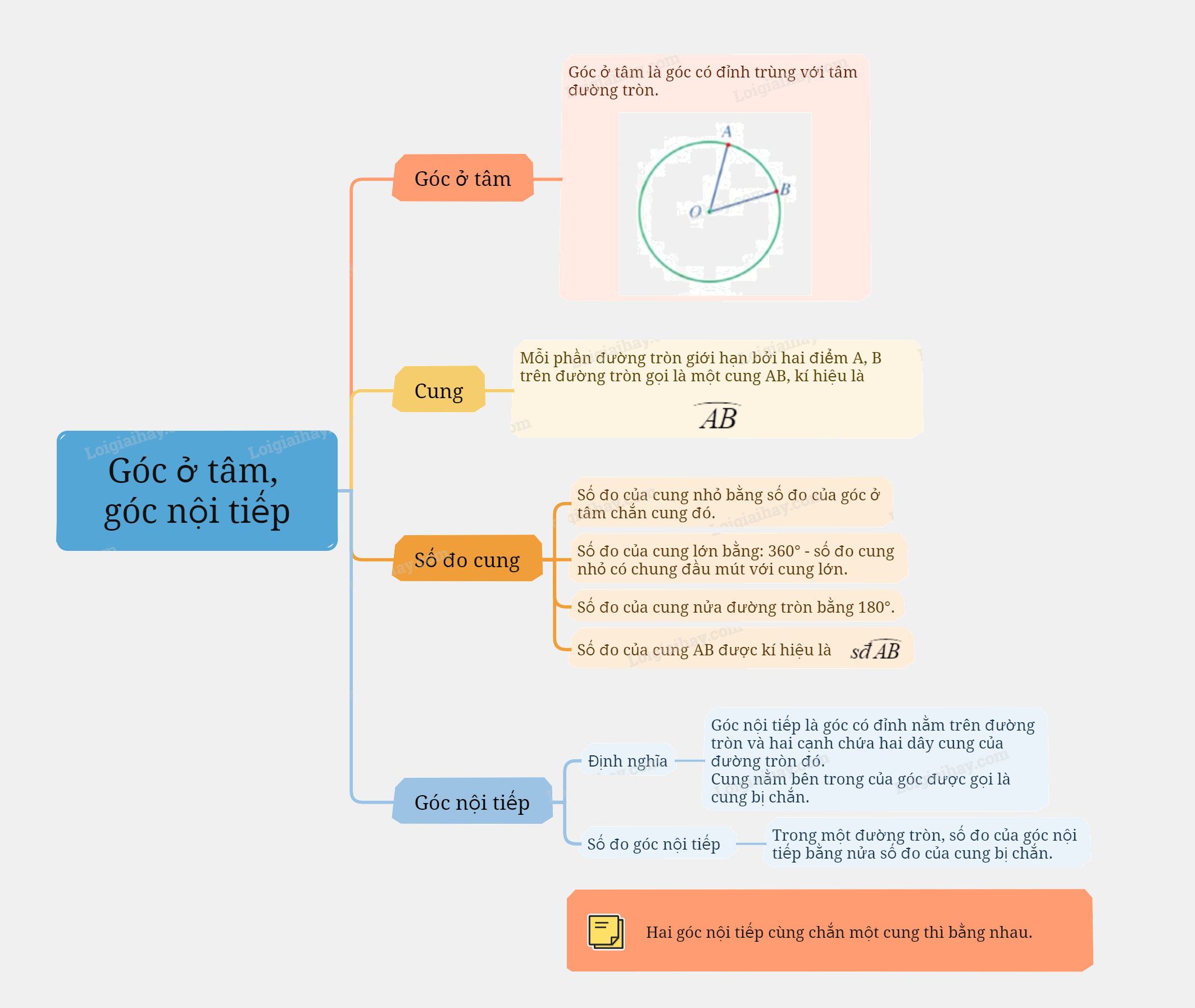
1. Góc ở tâm Định nghĩa Góc ở tâm là góc có đỉnh trùng với tâm đường tròn.
1. Góc ở tâm
Định nghĩa
Góc ở tâm là góc có đỉnh trùng với tâm đường tròn. |
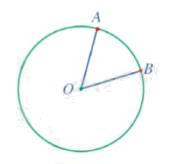
Nhận xét: Đường kính chia đường tròn thành hai phần, mỗi phần được gọi là một nửa đường tròn.
2. Cung, số đo cung
Cung
Phần đường tròn nối liền hai điểm A, B trên đường tròn được gọi là một cung (hay cung tròn) AB, kí hiệu là $\overset\frown{AB}$.
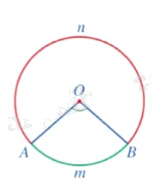
Góc ở tâm \(\widehat {AOB}\) chắn cung AnB hay cung AnB bị chắn bởi góc ở tâm \(\widehat {AOB}\).
$\overset\frown{AnB}$ là cung nhỏ và $\overset\frown{AmB}$ là cung lớn.
Số đo cung
- Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó. - Số đo của cung lớn bằng: \({360^0}\) - số đo cung nhỏ (có chung đầu mút với cung lớn). - Số đo của cung nửa đường tròn bằng \({180^0}\). - Số đo của cung AB được kí hiệu là sđ$\overset\frown{AB}$. |
Quy ước: Khi hai mút của cung trùng nhau, ta có “cung không” với số đo \({0^0}\) và cung cả đường tròn có số đo \({360^0}\).
Nhận xét: Góc ở tâm chắn một cung mà cung đó là nửa đường tròn thì có số đo bằng \({180^0}\).
Nếu điểm C là một điểm nằm trên cung AB thì sđ$\overset\frown{ACB}$ = sđ$\overset\frown{AC}$ + sđ$\overset\frown{CB}$.
Chú ý:
- Khác với so sánh hai góc, ta chỉ so sánh hai cung trong một đường tròn hay trong hai đường tròn bằng nhau. Cụ thể:
+ Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau;
+ Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn.
Hai cung AB và CD bằng nhau được kí hiệu là $\overset\frown{AB}=\overset\frown{CD}$.
Cung EG nhỏ hơn cung HK được kí hiệu là $\overset\frown{EG}<\overset\frown{HK}$. Trong trường hợp này, ta cũng nói cung HK lớn hơn cung EG và kí hiệu là $\overset\frown{HK}>\overset\frown{EG}$.
- Cho điểm \(A\) thuộc đường tròn \((O)\) và số thực \(\alpha \) với \(0 < \alpha < 360\). Sử dụng thược thẳng và thước đo độ, ta vẽ điểm \(B\) thuộc đường tròn \((O)\) như sau:
+ Nếu \(0 < \alpha \le 180\) thì ta vẽ theo chiểu quay của kim đồng hồ góc ở tâm AOB có số đo bằng \({\alpha ^0}\). Khi đó sđ$\overset\frown{AmB}={{\alpha }^{0}}$
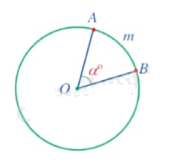
+ Nếu \(180 < \alpha \le 360\) thì ta vẽ theo ngược chiểu quay của kim đồng hồ góc ở tâm AOB có số đo bằng \({\alpha ^0} - {180^0}\). Khi đó sđ$\overset\frown{AnB}={{\alpha }^{0}}$.
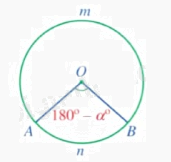
3. Góc nội tiếp
Định nghĩa
Góc nội tiếp là góc có đỉnh thuộc đường tròn và hai cạnh chứa hai dây cung của đường tròn đó. Cung nằm bên trong của góc được gọi là cung bị chắn. |
Định lí
Một góc ở tâm có số đo gấp hai lần số đo góc nội tiếp cùng chắn một cung. |
Số đo góc nội tiếp
Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn. Góc nội tiếp chắn nửa cung tròn có số đo bằng \({90^0}\). |
Ví dụ:
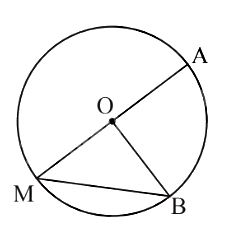
\(\widehat {AMB}\)là góc nội tiếp chắn $\overset\frown{AB}$ trên đường tròn (O) nên $\widehat{AMB}=\frac{1}{2}$sđ$\overset\frown{AB}$.
Nhận xét: Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau.
Trong chương trình Toán 9, kiến thức về góc ở tâm và góc nội tiếp đóng vai trò then chốt trong việc giải quyết các bài toán liên quan đến đường tròn. Bài viết này sẽ cung cấp một cách đầy đủ và chi tiết lý thuyết về hai loại góc này, cùng với các ví dụ minh họa và bài tập thực hành để giúp học sinh nắm vững kiến thức.
Định nghĩa: Góc ở tâm là góc có đỉnh là tâm của đường tròn và hai cạnh chứa hai bán kính.
Số đo: Số đo của góc ở tâm bằng số đo của cung bị chắn.
Ví dụ: Xét đường tròn (O) và cung AB. Góc AOB là góc ở tâm chắn cung AB. Nếu số đo cung AB là 60o thì số đo góc AOB cũng là 60o.
Định nghĩa: Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung.
Số đo: Số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
Ví dụ: Xét đường tròn (O) và điểm C nằm trên đường tròn. Góc ACB là góc nội tiếp chắn cung AB. Nếu số đo cung AB là 120o thì số đo góc ACB là 60o.
Góc ở tâm cùng chắn một cung thì có số đo bằng hai lần số đo của góc nội tiếp cùng chắn cung đó.
Công thức: ∠AOB = 2∠ACB (với A, B, C là các điểm trên đường tròn (O) và ∠AOB là góc ở tâm, ∠ACB là góc nội tiếp cùng chắn cung AB).
Bài 1: Cho đường tròn (O) có bán kính 5cm. Tính độ dài cung AB có số đo 72o.
Giải: Độ dài cung AB = (72/360) * 2πR = (72/360) * 2π * 5 = 2π (cm).
Bài 2: Cho đường tròn (O) và điểm A nằm trên đường tròn. Vẽ tiếp tuyến tại A và lấy điểm B trên tiếp tuyến đó. Nối OB cắt đường tròn tại C. Chứng minh rằng AC vuông góc với OB.
Giải: (Chứng minh dựa trên các tính chất của tiếp tuyến và góc nội tiếp).
Lý thuyết về góc ở tâm và góc nội tiếp có ứng dụng rộng rãi trong việc giải các bài toán hình học liên quan đến đường tròn, đặc biệt là trong việc tính toán các góc, độ dài cung và chứng minh các mối quan hệ giữa các điểm trên đường tròn.
Để nắm vững hơn lý thuyết, bạn nên luyện tập thêm các bài tập khác nhau với nhiều mức độ khó. Giaitoan.edu.vn cung cấp một hệ thống bài tập phong phú và đa dạng, giúp bạn rèn luyện kỹ năng giải toán một cách hiệu quả.
Hi vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và quan trọng về lý thuyết góc ở tâm và góc nội tiếp Toán 9 Cánh diều. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải các bài toán liên quan.