Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 1 - Cánh diều. Bài viết này sẽ hướng dẫn bạn từng bước giải bài tập 6 trang 11, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, hỗ trợ bạn giải quyết mọi khó khăn trong môn Toán.
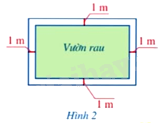
Trên một mảnh đất có dạng hình chữ nhật với chu vi bằng 52m. Trên mảnh đất đó, người ta làm một vườn có dạng hình chữ nhật có diện tích là (112{m^2}) và một lối đi xung quanh vườn rộng 1m (Hình 2). Tính các kích thuóc của mảnh đất đó.
Đề bài
Trên một mảnh đất có dạng hình chữ nhật với chu vi bằng 52m. Trên mảnh đất đó, người ta làm một vườn có dạng hình chữ nhật có diện tích là \(112{m^2}\) và một lối đi xung quanh vườn rộng 1m (Hình 2). Tính các kích thước của mảnh đất đó.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+ Gọi ẩn \(x\). Tìm điều kiện và đơn vị của ẩn.
+ Biểu diễn các đại lượng thông qua \(x\).
+ Tìm phương trình liên hệ.
+ Giải phương trình.
+ Đối chiếu với điều kiện của \(x\).
+ Kết luận bài toán.
Lời giải chi tiết
Nửa chu vi của mảnh đất là: \(52:2 = 26\left( m \right)\)
Gọi chiều dài của mảnh đất là \(x\left( {m,2 < x < 26} \right)\).
Chiều rộng của mảnh đất là: \(26 - x\,\left( m \right)\)
Chiều dài của vườn rau là: \(x - 1 - 1 = x - 2\,\,\left( m \right)\)
Chiều rộng của vườn rau là: \(26 - x - 1 - 1 = 24 - x\,\,\left( m \right)\)
Do diện tích của vườn rau là \(112{m^2}\) nên ta có phương trình:
\(\left( {x - 2} \right)\left( {24 - x} \right) = 112\)
\(24x - {x^2} - 48 + 2x - 112 = 0\)
\( - {x^2} + 26x - 160 = 0\)
\({x^2} - 26x + 160 = 0\)
\({\left( {x - 13} \right)^2} - 9 = 0\)
\(\left( {x - 13 - 3} \right)\left( {x - 13 + 3} \right) = 0\)
\(\left( {x - 16} \right)\left( {x - 10} \right) = 0\).
Để giải phương trình trên, ta giải hai phương trình sau:
*) \(x - 16 = 0\)
\(x = 16\);
*) \(x - 10 = 0\)
\(x = 10\).
Vậy chiều dài của mảnh đất là \(16\left( m \right)\)
Chiều rộng của mảnh đất là \(10\left( m \right)\)
Bài tập 6 trang 11 SGK Toán 9 tập 1 - Cánh diều thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để xác định hệ số góc và đường thẳng song song, vuông góc.
Bài tập 6 bao gồm các câu hỏi nhỏ, yêu cầu học sinh:
Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Câu a: Cho hàm số y = (m - 1)x + 3. Tìm giá trị của m để hàm số là hàm số bậc nhất.
Để hàm số y = (m - 1)x + 3 là hàm số bậc nhất, thì hệ số a phải khác 0. Do đó, m - 1 ≠ 0, suy ra m ≠ 1.
Câu b: Cho hàm số y = 2x - 1. Tìm hệ số góc của đường thẳng biểu diễn hàm số.
Hệ số góc của đường thẳng y = 2x - 1 là a = 2.
Câu c: Cho hai đường thẳng y = 3x + 2 và y = (k - 1)x + 5. Tìm giá trị của k để hai đường thẳng song song.
Để hai đường thẳng song song, thì hệ số góc của chúng phải bằng nhau. Do đó, 3 = k - 1, suy ra k = 4.
Câu d: Cho hai đường thẳng y = -x + 1 và y = (2k + 1)x - 3. Tìm giá trị của k để hai đường thẳng vuông góc.
Để hai đường thẳng vuông góc, thì tích hệ số góc của chúng phải bằng -1. Do đó, (-1) * (2k + 1) = -1, suy ra 2k + 1 = 1, suy ra k = 0.
Ví dụ 1: Tìm giá trị của m để đường thẳng y = (m + 2)x - 1 đi qua điểm A(1; 2).
Để đường thẳng đi qua điểm A(1; 2), thì tọa độ của điểm A phải thỏa mãn phương trình đường thẳng. Thay x = 1 và y = 2 vào phương trình, ta được:
2 = (m + 2) * 1 - 1
2 = m + 2 - 1
2 = m + 1
Suy ra m = 1.
Để củng cố kiến thức, bạn có thể tự giải các bài tập sau:
Bài tập 6 trang 11 SGK Toán 9 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và các tính chất của nó. Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải bài tập và đạt kết quả tốt trong môn Toán.