Bài học này cung cấp kiến thức nền tảng về đường tròn, các yếu tố liên quan và đặc biệt tập trung vào việc xác định vị trí tương đối giữa hai đường tròn. Nội dung được trình bày chi tiết, dễ hiểu, phù hợp với chương trình Toán 9 Cánh diều.
Chúng ta sẽ cùng nhau khám phá các khái niệm quan trọng, công thức tính toán và phương pháp giải bài tập liên quan đến chủ đề này. Mục tiêu là giúp bạn nắm vững lý thuyết và tự tin áp dụng vào giải quyết các bài toán thực tế.
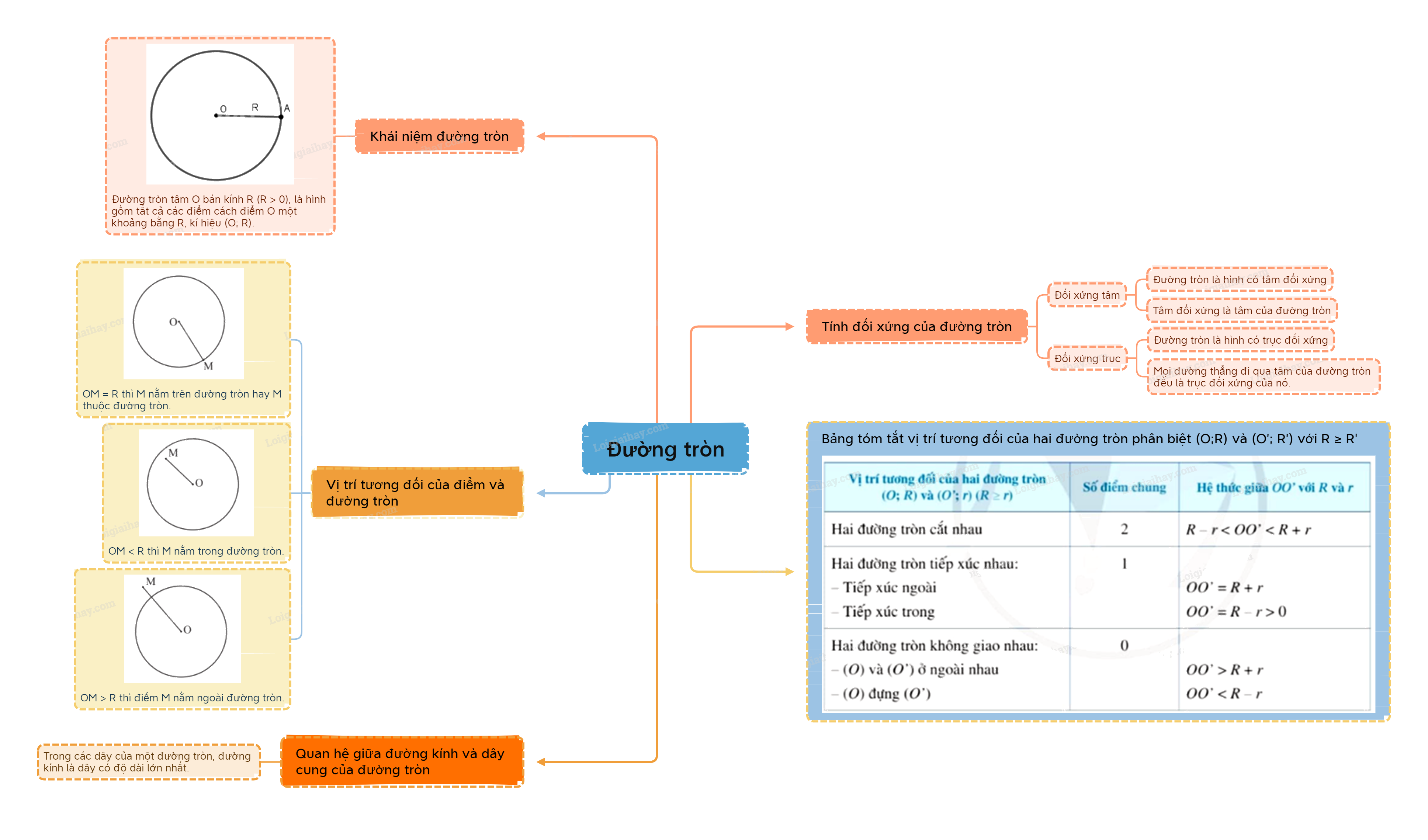
1. Khái niệm đường tròn Trong mặt phẳng, đường tròn tâm O bán kính R là tập hợp các điểm cách điểm O một khoảng bằng R (R > 0), kí hiệu là (O;R).
1. Khái niệm đường tròn
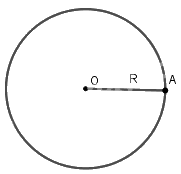
Trong mặt phẳng, đường tròn tâm O bán kính R là tập hợp các điểm cách điểm O một khoảng bằng R (R > 0), kí hiệu là (O;R). |
Chú ý:
- Một đường tròn hoàn toàn xác định khi biết tâm và bán kính.
- Khi không quan tâm đến bán kính của đường tròn (O;R), ta cũng có thể kí hiệu đường tròn là (O).
Vị trí tương đối của điểm và đường tròn
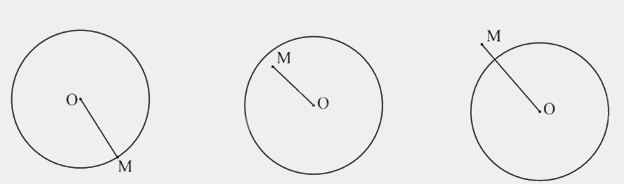
Cho đường tròn (O; R) và điểm M. Khi đó:
- Nếu điểm M thuộc đường tròn (O) (hay ta còn nói điểm M nằm trên đường tròn (O), hoặc đường tròn (O) đi qua điểm M) thì OM = R và ngược lại.
- Nếu điểm M nằm bên trong (hay nằm trong, ở trong) đường tròn (O) thì OM < R và ngược lại.
- Nếu điểm M nằm bên ngoài (hay nằm ngoài, ở ngoài) đường tròn (O) thì OM > R và ngược lại.
2. Liên hệ giữa đường kính và dây của đường tròn
Chú ý:
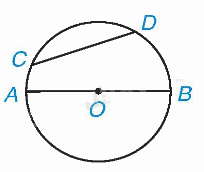
- Đoạn thẳng nối hai điểm phân biệt thuộc đường tròn được gọi là dây (hay dây cung) của đường tròn.
- Dây đi qua tâm là đường kính của đường tròn. Trong các dây của đường tròn, dây lớn nhất là đường kính.
Ví dụ: Cho hai điểm C, D cùng thuộc một đường tròn. Đoạn thẳng CD gọi là dây cung hoặc dây. Đường kính AB là một dây đi qua tâm.
3. Tính đối xứng của đường tròn
Nhận xét: Điểm đối xứng của một điểm tùy ý trên đường tròn qua tâm của đường tròn cũng nằm trên đường tròn đó.
Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó. |
Nhận xét: Điểm đối xứng của một điểm tùy ý trên đường tròn qua một đường thẳng đi qua tâm của đường tròn cũng nằm trên đường tròn đó.
Đường tròn là hình có trục đối xứng. Mỗi đường thẳng đi qua tâm là một trục đối xứng của đường tròn đó. |
Ví dụ:
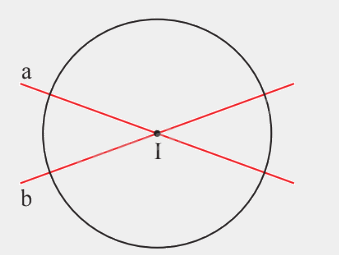
Hình tròn tâm I có:
I là tâm đối xứng;
Đường thẳng a, b là các trục đối xứng của hình tròn (I).
4. Vị trí tương đối của hai đường tròn
Hai đường tròn cắt nhau
Hai đường tròn có đúng hai điểm chung gọi là hai đường tròn cắt nhau.
|
Mỗi điểm chung của hai đường tròn cắt nhau được gọi là một giao điểm của hai đường tròn đó.
Nếu hai đường tròn (O;R) và (O’;r) với \(R \ge r\) cắt nhau thì \(R - r < OO' < R + r\).
Hai đường tròn tiếp xúc nhau
Hai đường tròn có đúng một điểm chung gọi là hai đường tròn tiếp xúc nhau (tại điểm chung đó). |
Điểm chung của hai đường tròn tiếp xúc nhau được gọi là tiếp điểm.
Có hai trường hợp về hai đường tròn tiếp xúc nhau:
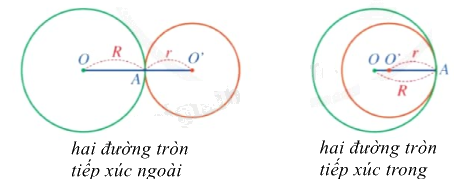
Nếu hai đường tròn (O;R) và (O’;r) tiếp xúc ngoài thì tiếp điểm A nằm giữa O, O’ và \(OO' = R + r\). Điều ngược lại cũng đúng.
Với R > r, nếu hai đường tròn (O;R) và (O’;r) tiếp xúc trong thì điểm O’ nằm giữa O, A và \(OO' = R - r\). Điều ngược lại cũng đúng.
Hai đường tròn không giao nhau
Hai đường tròn không có điểm chung gọi là hai đường tròn không giao nhau. |
Có hai trường hợp về hai đường tròn không giao nhau:
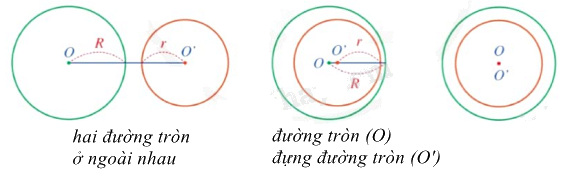
Nếu hai đường tròn (O;R) và (O’;r) ở ngoài nhau thì \(OO' > R + r\). Điều ngược lại cũng đúng.
Với R > r, nếu đường tròn (O) đựng đường tròn (O’) thì \(OO' > R - r\). Điều ngược lại cũng đúng.
Nhận xét: Ta có thể nhận biết vị trí tương đối của hai đường tròn \(\left( {O;R} \right),\left( {O';r} \right)\left( {R \ge r} \right)\) thông qua hệ thức liên hệ giữa OO’ với R và r được tóm tắt trong bảng sau:
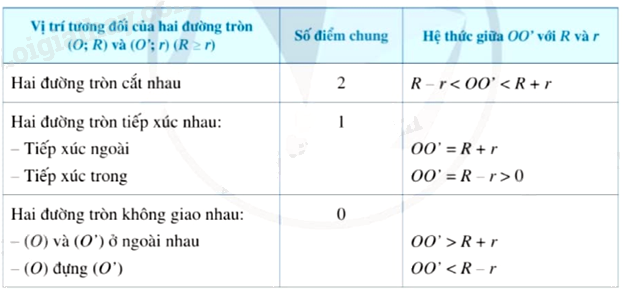
Ví dụ 1: Cho OO’ = 5cm, khi đó hai đường tròn (O;4cm) và (O’;3cm) cắt nhau vì:
4cm – 3cm = 1cm < 5cm < 7cm = 4cm + 3cm.
Ví dụ 2: Cho OO’ = 5cm, khi đó hai đường tròn (O;3cm) và (O’;2cm) tiếp xúc ngoài với nhau vì 5cm = 3cm + 2cm.
Cho OO’ = 3cm, khi đó hai đường tròn (O;8cm) và (O’;5cm) tiếp xúc trong với nhau vì 3cm = 8cm - 5cm.
Ví dụ 3: Cho đường tròn (O;3cm) và (O’;4cm) có \(OO' > 8cm\) thì \(OO' = 8cm > 3cm + 4cm = R + R'\) nên (O;3cm) và (O’;4cm) là hai đường tròn ngoài nhau.
Đường tròn là một trong những hình học cơ bản và quan trọng trong chương trình Toán 9. Việc nắm vững lý thuyết về đường tròn, đặc biệt là vị trí tương đối của hai đường tròn, là nền tảng để giải quyết nhiều bài toán hình học phức tạp.
Trước khi đi sâu vào vị trí tương đối của hai đường tròn, chúng ta cần ôn lại một số khái niệm cơ bản:
Xét hai đường tròn (O; R) và (O'; R'). Vị trí tương đối của hai đường tròn được xác định dựa trên khoảng cách d giữa hai tâm O và O' so với tổng và hiệu hai bán kính R và R'.
Ví dụ 1: Cho hai đường tròn (O; 3cm) và (O'; 5cm). Biết khoảng cách giữa hai tâm là 7cm. Xác định vị trí tương đối của hai đường tròn.
Giải: Ta có d = 7cm, R = 3cm, R' = 5cm. Vì d = R + R' (7 = 3 + 5) nên hai đường tròn tiếp xúc ngoài.
Ví dụ 2: Cho hai đường tròn (O; 4cm) và (O'; 2cm). Biết khoảng cách giữa hai tâm là 1cm. Xác định vị trí tương đối của hai đường tròn.
Giải: Ta có d = 1cm, R = 4cm, R' = 2cm. Vì d < |R - R'| (1 < |4 - 2| = 2) nên đường tròn (O'; 2cm) nằm hoàn toàn trong đường tròn (O; 4cm).
Lý thuyết về vị trí tương đối của hai đường tròn có ứng dụng rộng rãi trong việc giải các bài toán hình học, đặc biệt là các bài toán liên quan đến tiếp tuyến, dây cung và các yếu tố khác của đường tròn. Việc hiểu rõ lý thuyết này giúp chúng ta tiếp cận và giải quyết các bài toán một cách hiệu quả và chính xác.
Để nắm vững kiến thức về lý thuyết Đường tròn và vị trí tương đối của hai đường tròn, bạn nên thực hành giải nhiều bài tập khác nhau. Hãy tìm kiếm các bài tập trong sách giáo khoa, sách bài tập hoặc trên các trang web học toán online như giaitoan.edu.vn để luyện tập và củng cố kiến thức.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết Đường tròn và vị trí tương đối của hai đường tròn Toán 9 Cánh diều. Chúc bạn học tập tốt!