Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 80 và 81 sách giáo khoa Toán 9 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
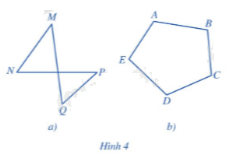
Tứ giác MNPQ ở Hình 4a gồm 4 đỉnh M, N, P, Q và 4 cạnh MN, NP, PQ, QM. Ngũ giác ABCDE gồm 5 đỉnh A, B, C, D, E và 5 cạnh AB, BC, CD, DE, EA. Quan sát hai hình đó, hãy cho biết các phát biểu sau là đúng hay sai: a) Mỗi đỉnh là điểm chung của đúng hai cạnh. b) Không có hai cạnh nào nằm trên cùng một đường thẳng.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 80 SGK Toán 9 Cánh diều
Tứ giác MNPQ ở Hình 4a gồm 4 đỉnh M, N, P, Q và 4 cạnh MN, NP, PQ, QM. Ngũ giác ABCDE gồm 5 đỉnh A, B, C, D, E và 5 cạnh AB, BC, CD, DE, EA. Quan sát hai hình đó, hãy cho biết các phát biểu sau là đúng hay sai:
a) Mỗi đỉnh là điểm chung của đúng hai cạnh.
b) Không có hai cạnh nào nằm trên cùng một đường thẳng.
Phương pháp giải:
a) Kiểm tra từng đỉnh của đa giác xem đỉnh đó có là điểm chung của đúng hai cạnh hay không?
b) Kiểm tra từng cạnh của đa giác xem cạnh đó có nằm trên cùng 1 đường thẳng với cạnh khác hay không.
Lời giải chi tiết:
a) Hình 4a: Đỉnh M là điểm chung của 2 cạnh MN, MQ; đỉnh N là điểm chung của 2 cạnh NP, NM; đỉnh P là điểm chung của 2 cạnh PN, PQ; đỉnh Q là điểm chung của 2 cạnh QM, QP.
Hình 4b: Đỉnh A là điểm chung của 2 cạnh AB, AE; đỉnh B là điểm chung của 2 cạnh BA, BC; đỉnh C là điểm chung của 2 cạnh CB, CD; đỉnh D là điểm chung của 2 cạnh DE, DC; đỉnh E là điểm chung của 2 cạnh EA, ED.
Vậy phát biểu “Mỗi đỉnh là điểm chung của đúng hai cạnh” là đúng.
b) Trong cả 2 hình, không có hai cạnh nào nằm trên cùng một đường thẳng.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 81 SGK Toán 9 Cánh diều
Nêu đặc điểm về vị trí của ngũ giác ABCDE so với đường thẳng chứa một cạnh bất kì của ngũ giác đó (Hình 5)

Phương pháp giải:
Ngũ giác ABCDE có nằm về một phía của đường thẳng chứa một cạnh bất kì của ngũ giác hay không?
Lời giải chi tiết:
Ngũ giác ABCDE luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của ngũ giác.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 80 SGK Toán 9 Cánh diều
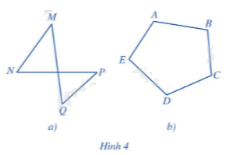
Tứ giác MNPQ ở Hình 4a gồm 4 đỉnh M, N, P, Q và 4 cạnh MN, NP, PQ, QM. Ngũ giác ABCDE gồm 5 đỉnh A, B, C, D, E và 5 cạnh AB, BC, CD, DE, EA. Quan sát hai hình đó, hãy cho biết các phát biểu sau là đúng hay sai:
a) Mỗi đỉnh là điểm chung của đúng hai cạnh.
b) Không có hai cạnh nào nằm trên cùng một đường thẳng.
Phương pháp giải:
a) Kiểm tra từng đỉnh của đa giác xem đỉnh đó có là điểm chung của đúng hai cạnh hay không?
b) Kiểm tra từng cạnh của đa giác xem cạnh đó có nằm trên cùng 1 đường thẳng với cạnh khác hay không.
Lời giải chi tiết:
a) Hình 4a: Đỉnh M là điểm chung của 2 cạnh MN, MQ; đỉnh N là điểm chung của 2 cạnh NP, NM; đỉnh P là điểm chung của 2 cạnh PN, PQ; đỉnh Q là điểm chung của 2 cạnh QM, QP.
Hình 4b: Đỉnh A là điểm chung của 2 cạnh AB, AE; đỉnh B là điểm chung của 2 cạnh BA, BC; đỉnh C là điểm chung của 2 cạnh CB, CD; đỉnh D là điểm chung của 2 cạnh DE, DC; đỉnh E là điểm chung của 2 cạnh EA, ED.
Vậy phát biểu “Mỗi đỉnh là điểm chung của đúng hai cạnh” là đúng.
b) Trong cả 2 hình, không có hai cạnh nào nằm trên cùng một đường thẳng.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 81 SGK Toán 9 Cánh diều
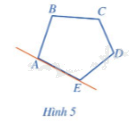
Nêu đặc điểm về vị trí của ngũ giác ABCDE so với đường thẳng chứa một cạnh bất kì của ngũ giác đó (Hình 5)
Phương pháp giải:
Ngũ giác ABCDE có nằm về một phía của đường thẳng chứa một cạnh bất kì của ngũ giác hay không?
Lời giải chi tiết:
Ngũ giác ABCDE luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của ngũ giác.
Mục 1 trang 80, 81 SGK Toán 9 tập 2 - Cánh diều tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc hai. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài tập này yêu cầu học sinh xác định chính xác các hệ số a, b, c của hàm số bậc hai cho trước. Lưu ý rằng hệ số a phải khác 0.
Ví dụ: Cho hàm số y = 2x2 - 5x + 1. Xác định a, b, c.
Giải: a = 2, b = -5, c = 1.
Để vẽ đồ thị hàm số bậc hai, ta thực hiện các bước sau:
Nếu a > 0 thì hàm số đạt giá trị nhỏ nhất tại đỉnh I(x0; y0). Giá trị nhỏ nhất là y0.
Nếu a < 0 thì hàm số đạt giá trị lớn nhất tại đỉnh I(x0; y0). Giá trị lớn nhất là y0.
Việc nắm vững kiến thức về hàm số bậc hai và rèn luyện kỹ năng giải bài tập là rất quan trọng đối với học sinh lớp 9. Hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể trong bài viết này, các em sẽ tự tin hơn khi giải các bài tập trong mục 1 trang 80, 81 SGK Toán 9 tập 2 - Cánh diều.
Chúc các em học tập tốt!