Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2, trang 119, 120 và 121 sách giáo khoa Toán 9 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Vẽ đường tròn (left( {O;2cm} right)) và các điểm (A,B) thỏa mãn (OA < 2cm,OB = 2cm). Nêu nhận xét về vị trí của các điểm (A,B) so với đường tròn (left( {O;2cm} right)).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 120 SGK Toán 9 Cánh diều
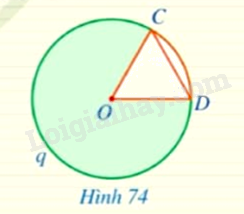
Cho hình quạt tròn \(COD\) giới hạn bởi hai bán kính \(OC,OD\) và cung \(CnD\) sao cho \(OC = OD\) (Hình 74). Hãy tìm số đo cung \(CqD\) ứng với hình quạt đó.
Phương pháp giải:
Chứng minh \(\Delta COD\) đều nên \(\widehat {COD} = {60^0}\).
Dựa vào tính chất góc ở tâm để tính số đo cung CqD.
Lời giải chi tiết:
Do OC = OD nên tam giác COD là tam giác đều, suy ra \(\widehat {COD} = {60^0}\).
Vì góc COD là góc ở tâm chắn cung nhỏ CD nên sđ$\overset\frown{CD}={{60}^{o}}$.
Suy ra sđ$\overset\frown{CqD}=360^o -sđ\overset\frown{CD} = 360^o -{{60}^{o}} = 300^o$.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 119 SGK Toán 9 Cánh diều
Vẽ đường tròn \(\left( {O;2cm} \right)\) và các điểm \(A,B\) thỏa mãn \(OA < 2cm,OB = 2cm\). Nêu nhận xét về vị trí của các điểm \(A,B\) so với đường tròn \(\left( {O;2cm} \right)\).
Phương pháp giải:
Dựa vào hình ảnh trực quan và các kiến thức đã học để trả lời bài toán.
Lời giải chi tiết:
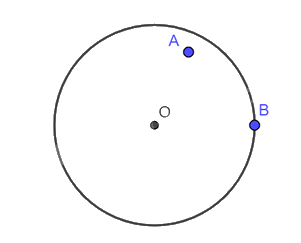
+ Điểm \(A\) nằm trong đường tròn \(\left( {O;2cm} \right)\).
+ Điểm \(B\) nằm trên đường tròn \(\left( {O;2cm} \right)\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 120 SGK Toán 9 Cánh diều
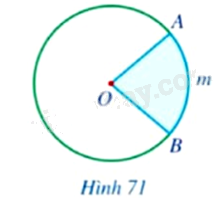
Quan sát Hình 71, hãy cho biết phần hình tròn \(\left( O \right)\) tô màu xanh được giới hạn bởi hai bán kính và cung nào?
Phương pháp giải:
Dựa vào hình ảnh trực quan để nhận xét.
Lời giải chi tiết:
Phần hình tròn \(\left( O \right)\) tô màu xanh được giới hạn bởi hai bán kính và cung $\overset\frown{AmB}$.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 5 trang 120 SGK Toán 9 Cánh diều
Ta coi mỗi hình tròn bán kính \(R\) là một hình quạt có số đo \(360^\circ \). Tính diện tích hình quạt tròn tâm \(O\), bán kính \(R\), biết số đo cung ứng với hình quạt tròn đó là:
a) \(1^\circ \)
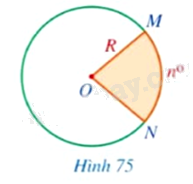
b) \(n^\circ \) (Hình 75).
Phương pháp giải:
Dựa vào kiến thức vừa học để tính.
Lời giải chi tiết:
a) Diện tích hình tròn là: \(S = \pi {R^2}\).
Diện tích hình quạt tròn tâm \(O\), bán kính \(R\), có số đo cung là \(1^\circ \) là: \(S = \frac{{\pi {R^2}}}{{360}}\).
b) Diện tích hình quạt tròn tâm \(O\), bán kính \(R\), có số đo cung là \(n^\circ \) là: \(S = \frac{{\pi {R^2}n}}{{360}}\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 119 SGK Toán 9 Cánh diều
Vẽ đường tròn \(\left( {O;2cm} \right)\) và các điểm \(A,B\) thỏa mãn \(OA < 2cm,OB = 2cm\). Nêu nhận xét về vị trí của các điểm \(A,B\) so với đường tròn \(\left( {O;2cm} \right)\).
Phương pháp giải:
Dựa vào hình ảnh trực quan và các kiến thức đã học để trả lời bài toán.
Lời giải chi tiết:
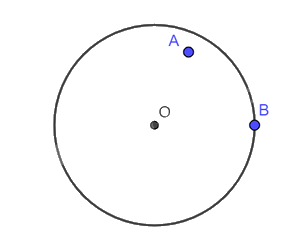
+ Điểm \(A\) nằm trong đường tròn \(\left( {O;2cm} \right)\).
+ Điểm \(B\) nằm trên đường tròn \(\left( {O;2cm} \right)\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 120 SGK Toán 9 Cánh diều
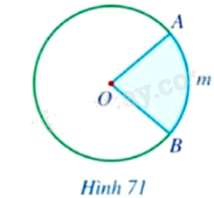
Quan sát Hình 71, hãy cho biết phần hình tròn \(\left( O \right)\) tô màu xanh được giới hạn bởi hai bán kính và cung nào?
Phương pháp giải:
Dựa vào hình ảnh trực quan để nhận xét.
Lời giải chi tiết:
Phần hình tròn \(\left( O \right)\) tô màu xanh được giới hạn bởi hai bán kính và cung $\overset\frown{AmB}$.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 120 SGK Toán 9 Cánh diều
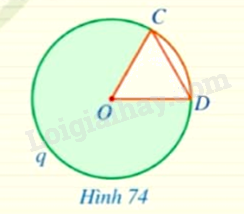
Cho hình quạt tròn \(COD\) giới hạn bởi hai bán kính \(OC,OD\) và cung \(CnD\) sao cho \(OC = OD\) (Hình 74). Hãy tìm số đo cung \(CqD\) ứng với hình quạt đó.
Phương pháp giải:
Chứng minh \(\Delta COD\) đều nên \(\widehat {COD} = {60^0}\).
Dựa vào tính chất góc ở tâm để tính số đo cung CqD.
Lời giải chi tiết:
Do OC = OD nên tam giác COD là tam giác đều, suy ra \(\widehat {COD} = {60^0}\).
Vì góc COD là góc ở tâm chắn cung nhỏ CD nên sđ$\overset\frown{CD}={{60}^{o}}$.
Suy ra sđ$\overset\frown{CqD}=360^o -sđ\overset\frown{CD} = 360^o -{{60}^{o}} = 300^o$.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 5 trang 120 SGK Toán 9 Cánh diều
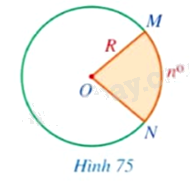
Ta coi mỗi hình tròn bán kính \(R\) là một hình quạt có số đo \(360^\circ \). Tính diện tích hình quạt tròn tâm \(O\), bán kính \(R\), biết số đo cung ứng với hình quạt tròn đó là:
a) \(1^\circ \)
b) \(n^\circ \) (Hình 75).
Phương pháp giải:
Dựa vào kiến thức vừa học để tính.
Lời giải chi tiết:
a) Diện tích hình tròn là: \(S = \pi {R^2}\).
Diện tích hình quạt tròn tâm \(O\), bán kính \(R\), có số đo cung là \(1^\circ \) là: \(S = \frac{{\pi {R^2}}}{{360}}\).
b) Diện tích hình quạt tròn tâm \(O\), bán kính \(R\), có số đo cung là \(n^\circ \) là: \(S = \frac{{\pi {R^2}n}}{{360}}\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 4 trang 121 SGK Toán 9 Cánh diều
Hình quạt tô màu đỏ ở Hình 65 có bán kính bằng 2 dm và góc ở tâm bằng \(150^\circ \).

a) Tính diện tích của hình quạt đó theo đơn vị decimét vuông (làm tròn kết quả đến hàng phần trăm).
b) Tính chiều dài cung tương ứng với hình quạt tròn đó.
Phương pháp giải:
Dựa vào công thức:
+ \(S = \frac{{\pi {R^2}n}}{{360}}\) để tính diện tích của hình quạt.
+ \(l = \frac{{\pi Rn}}{{180}}\) để tính chiều dài cung tương ứng.
Lời giải chi tiết:
a) Diện tích của hình quạt đó là:
\(S = \frac{{\pi .{2^2}.150}}{{360}} \approx 5,24\left( {d{m^2}} \right)\).
b) Chiều dài cung tương ứng với hình quạt tròn đó là:
\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .2.150}}{{180}} = \frac{{5\pi }}{3}\left( {dm} \right)\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 4 trang 121 SGK Toán 9 Cánh diều
Hình quạt tô màu đỏ ở Hình 65 có bán kính bằng 2 dm và góc ở tâm bằng \(150^\circ \).

a) Tính diện tích của hình quạt đó theo đơn vị decimét vuông (làm tròn kết quả đến hàng phần trăm).
b) Tính chiều dài cung tương ứng với hình quạt tròn đó.
Phương pháp giải:
Dựa vào công thức:
+ \(S = \frac{{\pi {R^2}n}}{{360}}\) để tính diện tích của hình quạt.
+ \(l = \frac{{\pi Rn}}{{180}}\) để tính chiều dài cung tương ứng.
Lời giải chi tiết:
a) Diện tích của hình quạt đó là:
\(S = \frac{{\pi .{2^2}.150}}{{360}} \approx 5,24\left( {d{m^2}} \right)\).
b) Chiều dài cung tương ứng với hình quạt tròn đó là:
\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .2.150}}{{180}} = \frac{{5\pi }}{3}\left( {dm} \right)\).
Mục 2 của chương trình Toán 9 tập 1 - Cánh diều tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc nhất. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài tập này yêu cầu học sinh xác định các yếu tố của hàm số bậc nhất (hệ số a, b), vẽ đồ thị hàm số, và tìm các điểm thuộc đồ thị. Để giải bài tập này, học sinh cần nắm vững định nghĩa hàm số bậc nhất, các tính chất của đồ thị hàm số, và các phương pháp vẽ đồ thị.
Bài tập này đưa ra các bài toán thực tế liên quan đến hàm số bậc nhất, yêu cầu học sinh xây dựng mô hình toán học và giải quyết bài toán. Để giải bài tập này, học sinh cần khả năng phân tích bài toán, xác định các yếu tố liên quan, và xây dựng phương trình hàm số phù hợp.
Bài tập này cung cấp một loạt các câu hỏi trắc nghiệm về hàm số bậc nhất, giúp học sinh kiểm tra và củng cố kiến thức đã học. Học sinh nên làm bài tập này một cách cẩn thận và tự giác đánh giá kết quả của mình.
Dưới đây là hướng dẫn giải chi tiết cho từng bài tập trong mục 2, trang 119, 120 và 121 SGK Toán 9 tập 1 - Cánh diều:
Câu 1: Hàm số y = 2x + 1 là hàm số...
Đáp án: A. Hàm số y = 2x + 1 có dạng y = ax + b, với a = 2 và b = 1, do đó là hàm số bậc nhất.
Hy vọng rằng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết các bài tập trong mục 2, trang 119, 120 và 121 SGK Toán 9 tập 1 - Cánh diều. Chúc các em học tập tốt!