Giải mục 2 trang 112, 113, 114 SGK Toán 9 tập 1 - Cánh diều

Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2, trang 112, 113 và 114 sách giáo khoa Toán 9 tập 1 - Cánh diều.

Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.

Quan sát góc ở tâm (AOB) (khác góc bẹt) ở Hình 48, cho biết trong hai phần đường tròn được tô màu xanh và màu đỏ, phần nào nằm bên trong, phần nào nằm bên ngoài góc (AOB).

HĐ2

Video hướng dẫn giải

Trả lời câu hỏi Hoạt động 2 trang 112 SGK Toán 9 Cánh diều

Quan sát góc ở tâm $AOB$ (khác góc bẹt) ở Hình 48, cho biết trong hai phần đường tròn được tô màu xanh và màu đỏ, phần nào nằm bên trong, phần nào nằm bên ngoài góc $AOB$.

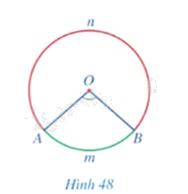
Giải mục 2 trang 112, 113, 114 SGK Toán 9 tập 1 - Cánh diều 0 1

Phương pháp giải:

Dựa vào hình ảnh trực quan để đưa ra nhận xét.

Lời giải chi tiết:

+ Phần được tô màu xanh nằm bên trong góc $AOB$.

+ Phần được tô màu đỏ nằm bên ngoài góc $AOB$.

LT2

Video hướng dẫn giải

Trả lời câu hỏi Luyện tập 2 trang 114 SGK Toán 9 Cánh diều

Trong Hình 53, tìm số đo của các góc ở tâm $\widehat {BOC};\widehat {DOA}$.

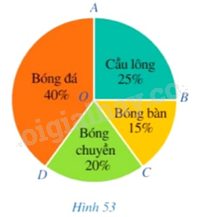
Giải mục 2 trang 112, 113, 114 SGK Toán 9 tập 1 - Cánh diều 1 1

Phương pháp giải:

Dựa vào kiến thức vừa học về số đo ở tâm để tính.

Lời giải chi tiết:

- Do số học sinh chọn môn Bóng bàn chiếm 15% số lượng học sinh nên số đo cung nhỏ $BC$ bằng 15% số đo của cung cả đường tròn.

Vì thế, sđ$\overset\frown{BC}=\frac{15}{100}.360{}^\circ =54{}^\circ $.

Vì số đo của cung nhỏ $BC$ bằng số đo của góc ở tâm $\widehat {BOC} = 54^\circ $.

- Do số học sinh chọn môn Bóng đá chiếm 40% số lượng học sinh nên số đo cung nhỏ $AD$ bằng 40% số đo của cung cả đường tròn.

Vì thế, sđ$\overset\frown{AD}=\frac{40}{100}.360{}^\circ =144{}^\circ $.

Vì số đo của cung nhỏ $AD$ bằng số đo của góc ở tâm $\widehat {DOA} = 144^\circ $.

Lựa chọn câu để xem lời giải nhanh hơn

HĐ2
LT2

Video hướng dẫn giải

Trả lời câu hỏi Hoạt động 2 trang 112 SGK Toán 9 Cánh diều

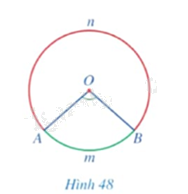
Giải mục 2 trang 112, 113, 114 SGK Toán 9 tập 1 - Cánh diều 1

Phương pháp giải:

Dựa vào hình ảnh trực quan để đưa ra nhận xét.

Lời giải chi tiết:

+ Phần được tô màu xanh nằm bên trong góc $AOB$.

+ Phần được tô màu đỏ nằm bên ngoài góc $AOB$.

Video hướng dẫn giải

Trả lời câu hỏi Luyện tập 2 trang 114 SGK Toán 9 Cánh diều

Trong Hình 53, tìm số đo của các góc ở tâm $\widehat {BOC};\widehat {DOA}$.

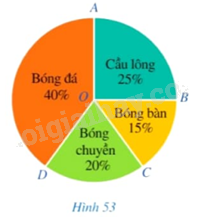
Giải mục 2 trang 112, 113, 114 SGK Toán 9 tập 1 - Cánh diều 2

Phương pháp giải:

Dựa vào kiến thức vừa học về số đo ở tâm để tính.

Lời giải chi tiết:

- Do số học sinh chọn môn Bóng bàn chiếm 15% số lượng học sinh nên số đo cung nhỏ $BC$ bằng 15% số đo của cung cả đường tròn.

Vì thế, sđ$\overset\frown{BC}=\frac{15}{100}.360{}^\circ =54{}^\circ $.

Vì số đo của cung nhỏ $BC$ bằng số đo của góc ở tâm $\widehat {BOC} = 54^\circ $.

- Do số học sinh chọn môn Bóng đá chiếm 40% số lượng học sinh nên số đo cung nhỏ $AD$ bằng 40% số đo của cung cả đường tròn.

Vì thế, sđ$\overset\frown{AD}=\frac{40}{100}.360{}^\circ =144{}^\circ $.

Vì số đo của cung nhỏ $AD$ bằng số đo của góc ở tâm $\widehat {DOA} = 144^\circ $.

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải mục 2 trang 112, 113, 114 SGK Toán 9 tập 1 - Cánh diều đặc sắc thuộc chuyên mục sgk toán 9 trên nền tảng toán. Với bộ bài tập toán trung học cơ sở được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải mục 2 trang 112, 113, 114 SGK Toán 9 tập 1 - Cánh diều: Tổng quan

Mục 2 trong SGK Toán 9 tập 1 - Cánh diều tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc nhất. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng vẽ đồ thị hàm số và xác định các yếu tố của hàm số.

Nội dung chi tiết các bài tập

Bài 1: Ôn tập về hàm số bậc nhất

Bài 1 yêu cầu học sinh nhắc lại định nghĩa hàm số bậc nhất, các dạng biểu diễn của hàm số bậc nhất (dạng tổng quát, dạng y = ax + b) và các tính chất của hàm số bậc nhất (hệ số a, đường thẳng song song, cắt nhau, vuông góc).

Câu a: Xác định hệ số a của hàm số y = (m-2)x + 3 để hàm số là hàm số bậc nhất.
Câu b: Tìm giá trị của m để hàm số y = (m-2)x + 3 đồng biến.
Câu c: Vẽ đồ thị của hàm số y = (m-2)x + 3 khi m = 3.

Lời giải:

Câu a: Để hàm số y = (m-2)x + 3 là hàm số bậc nhất, ta cần m - 2 ≠ 0, tức là m ≠ 2.
Câu b: Để hàm số y = (m-2)x + 3 đồng biến, ta cần m - 2 > 0, tức là m > 2.
Câu c: Khi m = 3, hàm số trở thành y = x + 3. Đồ thị của hàm số là một đường thẳng cắt trục Oy tại điểm (0, 3) và có hệ số góc là 1.

Bài 2: Bài tập về đồ thị hàm số bậc nhất

Bài 2 tập trung vào việc vẽ đồ thị hàm số bậc nhất và xác định các yếu tố của đồ thị (điểm đi qua, hệ số góc, giao điểm với các trục tọa độ).

Ví dụ: Vẽ đồ thị của hàm số y = -2x + 1 và xác định giao điểm của đồ thị với trục Ox.

Lời giải:

Xác định hai điểm thuộc đồ thị:
- Khi x = 0, y = 1. Vậy điểm A(0, 1) thuộc đồ thị.
- Khi y = 0, -2x + 1 = 0 => x = 1/2. Vậy điểm B(1/2, 0) thuộc đồ thị.
Vẽ đồ thị: Nối hai điểm A và B, ta được đồ thị của hàm số y = -2x + 1.
Xác định giao điểm với trục Ox: Giao điểm của đồ thị với trục Ox là điểm B(1/2, 0).

Bài 3: Ứng dụng hàm số bậc nhất vào giải toán thực tế

Bài 3 yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế liên quan đến các đại lượng thay đổi tuyến tính.

Ví dụ: Một người đi xe đạp với vận tốc 15 km/h. Hãy viết hàm số biểu thị quãng đường đi được của người đó theo thời gian đi.

Lời giải:

Gọi x là thời gian đi (giờ) và y là quãng đường đi được (km). Ta có hàm số y = 15x.

Lưu ý khi giải bài tập

Nắm vững định nghĩa và các tính chất của hàm số bậc nhất.
Rèn luyện kỹ năng vẽ đồ thị hàm số bậc nhất.
Vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Kiểm tra lại kết quả sau khi giải bài tập.

Kết luận

Hy vọng với lời giải chi tiết và dễ hiểu trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 2 trang 112, 113, 114 SGK Toán 9 tập 1 - Cánh diều. Chúc các em học tập tốt!