Bài học này cung cấp kiến thức nền tảng về đa giác đều, một khái niệm quan trọng trong hình học lớp 9. Chúng ta sẽ cùng nhau khám phá định nghĩa, tính chất đặc trưng và các công thức liên quan đến đa giác đều.
Ngoài ra, bài học còn đi sâu vào việc ứng dụng lý thuyết đa giác đều vào giải quyết các bài toán thực tế, giúp học sinh hiểu rõ hơn về vai trò của toán học trong cuộc sống.
1. Đa giác, đa giác lồi Đa giác Đa giác \({A_1}{A_2}...{A_n}\left( {n \ge 3;n \in \mathbb{N}} \right)\) là một hình gồm n đoạn thẳng \({A_1}{A_2},{A_2}{A_3},...,{A_{n - 1}}{A_n},{A_n}{A_1}\) sao cho mỗi điểm \({A_1},{A_2},...,{A_n}\) là điểm chung của đúng hai đoạn thẳng và không có hai đoạn thẳng nào nằm trên cùng một đường thẳng. Trong đa giác \({A_1}{A_2}...{A_n}\), các điểm \({A_1},{A_2},...,{A_n}\) là các đỉnh, các đoạn thẳng \({A_1}{A_2},{A_2}{A_3},...,{A_{n - 1}}{A_n},{A_n}{A_1}\) là c
1. Đa giác, đa giác lồi
Đa giác
Đa giác \({A_1}{A_2}...{A_n}\left( {n \ge 3;n \in \mathbb{N}} \right)\) là một hình gồm n đoạn thẳng \({A_1}{A_2},{A_2}{A_3},...,{A_{n - 1}}{A_n},{A_n}{A_1}\) sao cho mỗi điểm \({A_1},{A_2},...,{A_n}\) là điểm chung của đúng hai đoạn thẳng và không có hai đoạn thẳng nào nằm trên cùng một đường thẳng. Trong đa giác \({A_1}{A_2}...{A_n}\), các điểm \({A_1},{A_2},...,{A_n}\) là các đỉnh, các đoạn thẳng \({A_1}{A_2},{A_2}{A_3},...,{A_{n - 1}}{A_n},{A_n}{A_1}\) là các cạnh. |
Đa giác lồi
Đa giác lồi là đa giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của đa giác đó. |
Ví dụ:
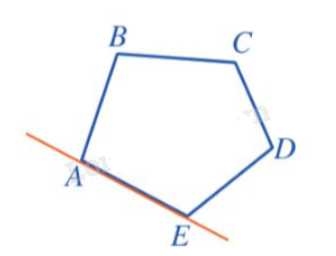
- Do ngũ giác ABCDE luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của ngũ giác đó nên ta nói ngũ giác ABCDE là ngũ giác lồi.
- Với ngũ giác lồi ABCDE, các góc ABC, BCD, CDE, DEA, EAB gọi là các góc của đa giác.
Trong trường hợp tổng quát, đa giác lồi có n cạnh (\(n \ge 3\), \(n \in N\)) cũng là đa giác lồi có n góc. Khi n lần lượt bằng 3; 4; 5; 6; ... ta có tam giác, tứ giác lồi, ngũ giác lồi, lục giác lồi, ...
Quy ước: Từ nay về sau, khi nói về đa giác mà không chú thích gì thêm thì ta hiểu đó là đa giác lồi.
2. Đa giác đều
Đa giác đều là một đa giác lồi có các cạnh bằng nhau và các góc bằng nhau. |
Ví dụ: Một số hình đa giác đều thường gặp trong hình học:
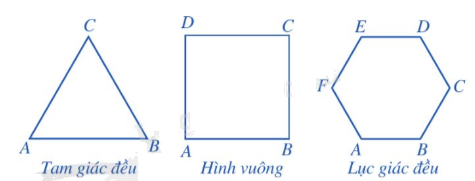
Nhận xét: Đối với mỗi tam giác đều, có đúng một điểm O cách đều tất cả các đỉnh của đa giác đó. Điểm O đó được gọi là tâm của đa giác đều.
Chú ý: Phần mặt phẳng giới hạn bởi đa giác đều được gọi là hình đa giác đều. Vì mỗi hình đa giác đều cũng là một phần của mặt phẳng nên hình đa giác đều còn gọi là hình phẳng đều.
3. Hình đa giác đều trong thực tiễn
Trong thế giới tự nhiên, trong nghệ thuật kiến trúc và thiết kế công nghệ, vật thể có hình ảnh liên quan đến hình đa giác đều rất đa dạng và phong phú.
Đa giác đều là một khái niệm quan trọng trong hình học, đặc biệt là ở chương trình Toán 9. Hiểu rõ về đa giác đều không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn mở ra cánh cửa để khám phá những ứng dụng thú vị của toán học trong thực tế.
Một đa giác được gọi là đa giác đều khi nó vừa là đa giác lồi vừa có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau. Nói cách khác, một đa giác đều là một đa giác có tính đối xứng cao.
Đa giác đều có nhiều tính chất quan trọng, bao gồm:
Chu vi (P): P = n * a (trong đó n là số cạnh, a là độ dài cạnh)
Diện tích (S): S = (n * a2) / (4 * tan(π/n)) hoặc S = (P * r) / 2 (trong đó r là apothem)
Đa giác đều xuất hiện rất nhiều trong thực tế, ví dụ:
Bài 1: Tính chu vi và diện tích của một hình lục giác đều có cạnh dài 5cm.
Giải:
Chu vi: P = 6 * 5 = 30cm
Diện tích: S = (6 * 52) / (4 * tan(π/6)) ≈ 64.95cm2
Để nắm vững kiến thức về đa giác đều, bạn nên thực hành giải nhiều bài tập khác nhau. Hãy tìm kiếm các bài tập trong sách giáo khoa, sách bài tập hoặc trên các trang web học toán online như giaitoan.edu.vn. Việc luyện tập thường xuyên sẽ giúp bạn hiểu rõ hơn về các khái niệm và công thức liên quan đến đa giác đều.
Lý thuyết Đa giác đều là một phần quan trọng của chương trình Toán 9. Việc hiểu rõ về đa giác đều không chỉ giúp bạn giải quyết các bài toán trong học tập mà còn mở ra những ứng dụng thú vị trong thực tế. Hãy dành thời gian để học tập và luyện tập để nắm vững kiến thức này nhé!