Giải bài tập 1 trang 117 SGK Toán 9 tập 1 - Cánh diều

Chào mừng các em học sinh đến với lời giải chi tiết bài tập 1 trang 117 SGK Toán 9 tập 1 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án và cách giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Bài tập này thuộc chương trình Toán 9 tập 1, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến hàm số bậc nhất. Các em hãy cùng theo dõi lời giải chi tiết dưới đây để hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.

Quan sát Hình 62, hãy cho biết: a) 6 góc ở tâm có hai cạnh lần lượt chứa hai trong bốn điểm (A,B,C,D); b) 4 góc nội tiếp có hai cạnh lần lượt chứa ba điểm trong bốn điểm.

Đề bài

Quan sát Hình 62, hãy cho biết:

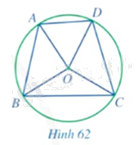
Giải bài tập 1 trang 117 SGK Toán 9 tập 1 - Cánh diều 1

a) 6 góc ở tâm có hai cạnh lần lượt chứa hai trong bốn điểm \(A,B,C,D\);

b) 4 góc nội tiếp có hai cạnh lần lượt chứa ba điểm trong bốn điểm.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài tập 1 trang 117 SGK Toán 9 tập 1 - Cánh diều 2

Dựa vào định nghĩa góc ở tâm, góc nội tiếp để trả lời.

Lời giải chi tiết

a) 6 góc ở tâm có hai cạnh lần lượt chứa hai trong bốn điểm \(A,B,C,D\) là: \(\widehat {AOB};\widehat {AOD};\widehat {AOC};\widehat {DOC};\widehat {DOB};\widehat {COB}\),

b) 4 góc nội tiếp có hai cạnh lần lượt chứa ba điểm trong bốn điểm là: \(\widehat {BAD};\widehat {ADC};\widehat {DCB};\widehat {CBA}\).

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài tập 1 trang 117 SGK Toán 9 tập 1 - Cánh diều đặc sắc thuộc chuyên mục sách bài tập toán 9 trên nền tảng học toán. Với bộ bài tập toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài tập 1 trang 117 SGK Toán 9 tập 1 - Cánh diều: Tổng quan

Bài tập 1 trang 117 SGK Toán 9 tập 1 - Cánh diều yêu cầu học sinh xác định hệ số a của hàm số bậc nhất y = ax + b khi biết đồ thị của hàm số đi qua hai điểm cho trước. Đây là một dạng bài tập cơ bản nhưng quan trọng, giúp học sinh hiểu rõ mối liên hệ giữa đồ thị và phương trình hàm số.

Phương pháp giải bài tập

Để giải bài tập này, chúng ta cần thực hiện các bước sau:

Bước 1: Thay tọa độ của hai điểm mà đồ thị hàm số đi qua vào phương trình y = ax + b.
Bước 2: Giải hệ phương trình hai ẩn a và b để tìm ra giá trị của a.
Bước 3: Kiểm tra lại kết quả bằng cách thay giá trị của a vào phương trình hàm số và xem đồ thị có đi qua hai điểm đã cho hay không.

Lời giải chi tiết bài tập 1 trang 117 SGK Toán 9 tập 1 - Cánh diều

Bài 1: Cho hàm số y = ax + b. Biết đồ thị của hàm số đi qua hai điểm A(0; -2) và B(2; 0). Hãy xác định hệ số a.

Giải:

Thay tọa độ điểm A(0; -2) vào phương trình y = ax + b, ta được: -2 = a * 0 + b => b = -2.
Thay tọa độ điểm B(2; 0) vào phương trình y = ax + b, ta được: 0 = a * 2 + b => 0 = 2a - 2.
Giải phương trình 2a - 2 = 0, ta được: a = 1.

Vậy, hệ số a của hàm số là 1.

Các dạng bài tập tương tự

Ngoài bài tập 1, các em có thể gặp các dạng bài tập tương tự như:

Xác định hệ số b của hàm số y = ax + b khi biết hệ số a và một điểm mà đồ thị đi qua.
Xác định phương trình hàm số y = ax + b khi biết hai điểm mà đồ thị đi qua.
Vẽ đồ thị của hàm số y = ax + b khi biết hệ số a và b.

Mẹo giải bài tập

Để giải các bài tập về hàm số bậc nhất một cách nhanh chóng và chính xác, các em nên:

Nắm vững phương trình đường thẳng và các yếu tố liên quan (hệ số góc, giao điểm với trục tọa độ).
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm vẽ đồ thị để kiểm tra kết quả.

Kết luận

Bài tập 1 trang 117 SGK Toán 9 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, các em sẽ tự tin hơn trong quá trình học tập và giải bài tập.