Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn giải bài tập 4 trang 92 SGK Toán 9 tập 1 - Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp tối ưu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
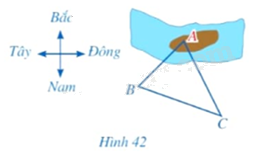
Một người đứng ở vị trí (B) trên bờ sông muốn sử dụng la bàn để ước lượng khoảng cách từ vị trí đó đến một vị trí (A) ở trên một cù lao giữa dòng sông. Người đó đã làm như sau: - Sử dụng la bàn, xác định được phương (BA) lệch với phương Nam – Bắc về hướng Đông (52^circ ). - Người đó di chuyển đến vị trí (C), cách (B) một khoảng là 187m. Sử dụng la bàn, xác định được phương (CA) lệch với phương Nam – Bắc về hướng Tây (27^circ ); (CB) lệch với phương Nam – Bắc về hướng Tây
Đề bài
Một người đứng ở vị trí \(B\) trên bờ sông muốn sử dụng la bàn để ước lượng khoảng cách từ vị trí đó đến một vị trí \(A\) ở trên một cù lao giữa dòng sông. Người đó đã làm như sau:
- Sử dụng la bàn, xác định được phương \(BA\) lệch với phương Nam – Bắc về hướng Đông \(52^\circ \).
- Người đó di chuyển đến vị trí \(C\), cách \(B\) một khoảng là 187m. Sử dụng la bàn, xác định được phương \(CA\) lệch với phương Nam – Bắc về hướng Tây \(27^\circ \); \(CB\) lệch với phương Nam – Bắc về hướng Tây \(70^\circ \) (Hình 42).
Em hãy giúp người đó tính khoảng cách \(AB\) từ những dữ liệu trên (làm tròn kết quả đến hàng đơn vị của mét).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào tỉ số lượng giác để giải bài toán.
Lời giải chi tiết
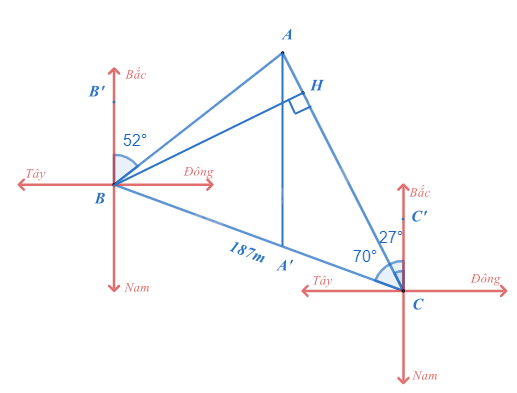
Lấy B’B, C’C là các đường thẳng biểu diễn phương Nam – Bắc như hình vẽ.
Theo bài ra ta có \(\widehat {B'BA} = 52^\circ ,\widehat {C'CA} = 27^\circ ,\widehat {C'CB} = 70^\circ \) suy ra \(\widehat {ACB} = \widehat {C'CB} - \widehat {C'CA} = 70^\circ - 27^\circ = 43^\circ \).
Kẻ AA’ ( \(A' \in BC\)) song song với phương Nam – Bắc, khi đó \(AA'//BB'//CC'\).
Vì \(AA'//BB'//CC'\) nên ta có \(\widehat {B'BA} = \widehat {BAA'} = 52^\circ \) (hai góc so le trong) và \(\widehat {A'AC} = \widehat {C'CA} = 27^\circ \) suy ra \(\widehat {BAC} = \widehat {BAA'} + \widehat {A'AC} = 52^\circ + 27^\circ = 79^\circ \).
Kẻ \(BH \bot AC\left( {H \in AC} \right)\).
Xét \(\Delta BHC\) vuông tại H có: \(\sin C = \frac{{BH}}{{BC}}\) suy ra \(BH = \sin C.BC = \sin 43^\circ .187 \approx 128\left( m \right)\).
Xét \(\Delta BAH\) vuông tại H có: \(\sin A = \frac{{BH}}{{BA}}\) suy ra \(BA = \frac{{BH}}{{\sin A}} \approx \frac{{128}}{{\sin 79^\circ }} \approx 130\left( m \right)\)
Vậy khoảng cách AB là khoảng 130m.
Bài tập 4 trang 92 SGK Toán 9 tập 1 - Cánh diều thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:
Để xác định một hàm số có phải là hàm số bậc nhất hay không, ta cần kiểm tra xem nó có dạng y = ax + b hay không, với a và b là các số thực và a ≠ 0. Trong bài tập này, ta cần phân tích các hàm số đã cho và xác định xem chúng có thỏa mãn điều kiện này hay không.
Sau khi xác định được hàm số bậc nhất, ta cần tìm hệ số a và b. Hệ số a cho biết độ dốc của đường thẳng, còn hệ số b cho biết tung độ gốc. Để tìm a và b, ta có thể sử dụng các phương pháp sau:
Nếu ta biết hai điểm thuộc đường thẳng, ta có thể thay tọa độ của hai điểm này vào phương trình y = ax + b để tìm a và b.
Nếu ta biết hệ số góc và tung độ gốc của đường thẳng, ta có thể thay trực tiếp các giá trị này vào phương trình y = ax + b.
Sau khi tìm được hệ số a và b, ta có thể vẽ đồ thị hàm số. Để vẽ đồ thị, ta cần xác định một vài điểm thuộc đường thẳng, sau đó nối các điểm này lại với nhau. Ta có thể sử dụng bảng giá trị để tìm các điểm thuộc đường thẳng.
Giả sử ta có hàm số y = 2x + 1. Để vẽ đồ thị hàm số này, ta có thể chọn hai điểm thuộc đường thẳng, ví dụ như điểm A(0, 1) và điểm B(1, 3). Sau đó, ta nối hai điểm này lại với nhau để được đồ thị hàm số.
Khi giải bài tập về hàm số bậc nhất, ta cần lưu ý những điều sau:
Để củng cố kiến thức về hàm số bậc nhất, bạn có thể làm thêm các bài tập tương tự sau:
Bài tập 4 trang 92 SGK Toán 9 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất. Hy vọng với hướng dẫn chi tiết này, bạn sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!
| Hàm số | Hệ số a | Hệ số b |
|---|---|---|
| y = 2x + 1 | 2 | 1 |
| y = -3x + 2 | -3 | 2 |