Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 86 và 87 sách giáo khoa Toán 9 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho điểm O cố định. a) Xét điểm M tùy ý (khác O) và đường tròn (O;OM). Hãy tìm điểm M’ thuộc đường tròn (O; OM) sao cho chiều quay từ tia OM đến tia OM’ cùng chiều quay của kim đồng hồ và cung MnM’ có số đo (120^circ .) b) Xét điểm N tùy ý (khác O) và đường tròn (O;ON). Hãy tìm điểm N’ thuộc đường tròn (O; ON) sao cho chiều quay từ tia ON đến tia ON’ ngược chiều quay của kim đồng hồ và cung NpN’ có số đo (300^circ .)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 86 SGK Toán 9 Cánh diều
Cho điểm O cố định.
a) Xét điểm M tùy ý (khác O) và đường tròn (O;OM). Hãy tìm điểm M’ thuộc đường tròn (O; OM) sao cho chiều quay từ tia OM đến tia OM’ cùng chiều quay của kim đồng hồ và cung MnM’ có số đo \(120^\circ .\)
b) Xét điểm N tùy ý (khác O) và đường tròn (O;ON). Hãy tìm điểm N’ thuộc đường tròn (O; ON) sao cho chiều quay từ tia ON đến tia ON’ ngược chiều quay của kim đồng hồ và cung NpN’ có số đo \(300^\circ .\)
Phương pháp giải:
Thực hiện vẽ theo yêu cầu
Lời giải chi tiết:
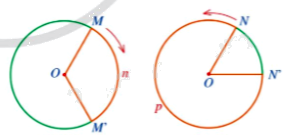
a)
- Vẽ đường (O; OM)
- Lấy điểm \( M' \in (O; OM)\) sao cho chiều quay từ tia OM đến tia OM' cùng chiều quay kim đồng hồ.
Xét đường (O; OM) có:
\( \widehat{MOM'} =\) số đo cung MM' \(= 120^\circ \)
b)
- Vẽ đường (O; ON)
- Lấy điểm \( N' \in (O; ON)\) sao cho chiều quay từ tia ON đến tia ON' ngược chiều quay kim đồng hồ.
Xét đường (O; ON) có:
\( \widehat{NON'} =\) số đo cung NN' \(= 360^\circ -\) số đo cung NpN' \)
\( = 360^\circ - 300^\circ = 60^\circ \)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 87 SGK Toán 9 Cánh diều
Cho hình vuông ABCD tâm O, chỉ ra phép quay thuận chiều tâm O sao cho phép quay đó biến mỗi điểm A, B, C, D thành điểm đối xứng với nó qua tâm O.
Phương pháp giải:
Bước 1: Xác định điểm đối xứng của mỗi điểm A, B, C, D qua tâm O.
Bước 2: Xác định phép quay \(a^\circ \) biến mỗi điểm thành điểm đối xứng với nó .
Lời giải chi tiết:
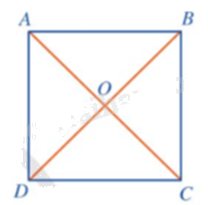
Điểm đối xứng của mỗi điểm A, B, C, D qua tâm O lần lượt là C, D, A, B.
Phép quay thuận chiều \(180^\circ \) tâm O sẽ biến mỗi điểm A, B, C, D thành điểm đối xứng với nó qua tâm O.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 86 SGK Toán 9 Cánh diều
Cho điểm O cố định.
a) Xét điểm M tùy ý (khác O) và đường tròn (O;OM). Hãy tìm điểm M’ thuộc đường tròn (O; OM) sao cho chiều quay từ tia OM đến tia OM’ cùng chiều quay của kim đồng hồ và cung MnM’ có số đo \(120^\circ .\)
b) Xét điểm N tùy ý (khác O) và đường tròn (O;ON). Hãy tìm điểm N’ thuộc đường tròn (O; ON) sao cho chiều quay từ tia ON đến tia ON’ ngược chiều quay của kim đồng hồ và cung NpN’ có số đo \(300^\circ .\)
Phương pháp giải:
Thực hiện vẽ theo yêu cầu
Lời giải chi tiết:
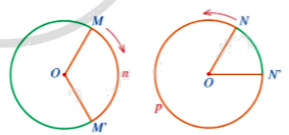
a)
- Vẽ đường (O; OM)
- Lấy điểm \( M' \in (O; OM)\) sao cho chiều quay từ tia OM đến tia OM' cùng chiều quay kim đồng hồ.
Xét đường (O; OM) có:
\( \widehat{MOM'} =\) số đo cung MM' \(= 120^\circ \)
b)
- Vẽ đường (O; ON)
- Lấy điểm \( N' \in (O; ON)\) sao cho chiều quay từ tia ON đến tia ON' ngược chiều quay kim đồng hồ.
Xét đường (O; ON) có:
\( \widehat{NON'} =\) số đo cung NN' \(= 360^\circ -\) số đo cung NpN' \)
\( = 360^\circ - 300^\circ = 60^\circ \)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 87 SGK Toán 9 Cánh diều
Cho hình vuông ABCD tâm O, chỉ ra phép quay thuận chiều tâm O sao cho phép quay đó biến mỗi điểm A, B, C, D thành điểm đối xứng với nó qua tâm O.
Phương pháp giải:
Bước 1: Xác định điểm đối xứng của mỗi điểm A, B, C, D qua tâm O.
Bước 2: Xác định phép quay \(a^\circ \) biến mỗi điểm thành điểm đối xứng với nó .
Lời giải chi tiết:
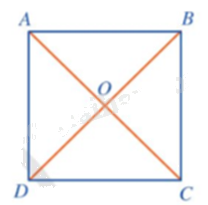
Điểm đối xứng của mỗi điểm A, B, C, D qua tâm O lần lượt là C, D, A, B.
Phép quay thuận chiều \(180^\circ \) tâm O sẽ biến mỗi điểm A, B, C, D thành điểm đối xứng với nó qua tâm O.
Mục 1 trang 86, 87 SGK Toán 9 tập 2 - Cánh diều tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc hai. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 1 yêu cầu học sinh xác định các hệ số a, b, c của hàm số bậc hai, tìm đỉnh của parabol, vẽ đồ thị hàm số và xác định khoảng đồng biến, nghịch biến của hàm số. Để giải bài tập này, học sinh cần nắm vững các công thức và định lý liên quan đến hàm số bậc hai.
Bài 2 đưa ra một bài toán thực tế liên quan đến hàm số bậc hai, yêu cầu học sinh xây dựng mô hình toán học và giải quyết bài toán đó. Ví dụ, bài toán có thể liên quan đến việc tìm quỹ đạo của một vật được ném lên, hoặc tìm kích thước tối ưu của một hình chữ nhật để có diện tích lớn nhất.
Để giải bài tập này, học sinh cần:
Bài 3 cung cấp một số câu hỏi trắc nghiệm để kiểm tra mức độ hiểu bài của học sinh. Các câu hỏi trắc nghiệm thường tập trung vào các kiến thức cơ bản về hàm số bậc hai, như xác định hệ số, tìm đỉnh, vẽ đồ thị và ứng dụng hàm số vào giải quyết bài toán.
Để giải tốt các bài tập trong mục 1 trang 86, 87 SGK Toán 9 tập 2 - Cánh diều, học sinh cần:
Hy vọng rằng với lời giải chi tiết và những lời khuyên hữu ích trên đây, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 1 trang 86, 87 SGK Toán 9 tập 2 - Cánh diều. Chúc các em học tập tốt!