Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng về vị trí tương đối giữa đường thẳng và đường tròn trong chương trình Toán 9 Cánh diều. Chúng ta sẽ cùng nhau khám phá các trường hợp có thể xảy ra và cách xác định chúng.
Nắm vững lý thuyết này là nền tảng để giải quyết các bài toán liên quan đến đường thẳng và đường tròn, đồng thời giúp bạn hiểu sâu hơn về hình học phẳng.
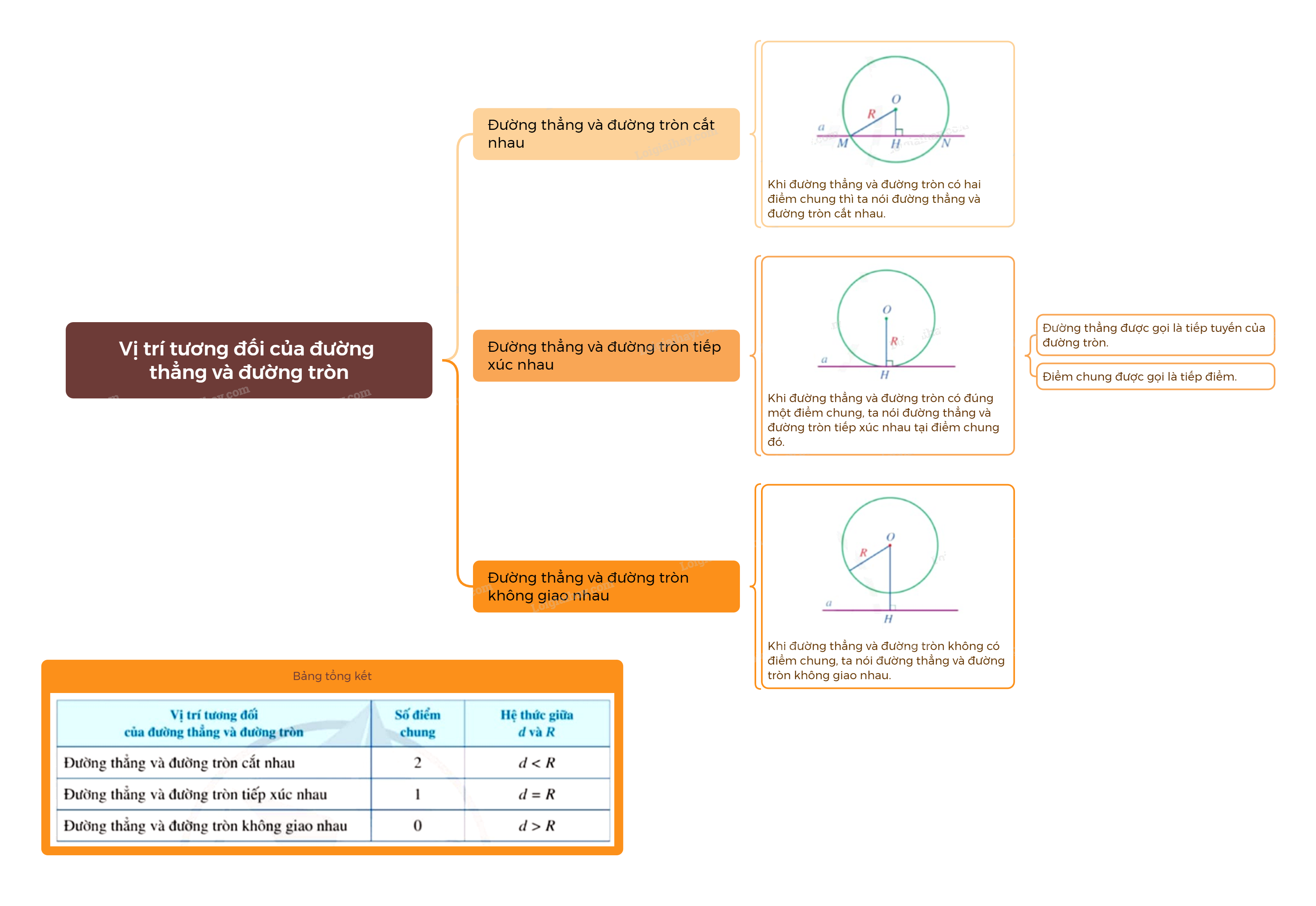
1. Đường thẳng và đường tròn cắt nhau Khi đường thẳng và đường tròn có hai điểm chung thì ta nói đường thẳng và đường tròn cắt nhau. Nếu đường thẳng và đường tròn cắt nhau thì mỗi điểm chung được gọi là một giao điểm.
1. Đường thẳng và đường tròn cắt nhau
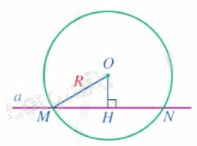
Khi đường thẳng và đường tròn có hai điểm chung thì ta nói đường thẳng và đường tròn cắt nhau. |
Nếu đường thẳng và đường tròn cắt nhau thì mỗi điểm chung được gọi là một giao điểm.
Nhận xét: Đường thẳng a cắt đường tròn (O;R) khi khoảng cách từ tâm O đến đường thẳng a nhỏ hơn R và ngược lại.
2. Đường thẳng và đường tròn tiếp xúc nhau
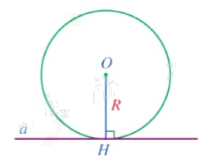
Khi đường thẳng và đường tròn có đúng một điểm chung, ta nói đường thẳng và đường tròn tiếp xúc nhau tại điểm chung đó. |
Nếu đường thẳng và đường tròn tiếp xúc nhau thì đường thẳng được gọi là tiếp tuyến của đường tròn, điểm chung được gọi là tiếp điểm.
Nhận xét: Đường thẳng a tiếp xúc với đường tròn (O;R) khi khoảng cách từ tâm O đến đường thẳng a bằng R và ngược lại.
3. Đường thẳng và đường tròn không giao nhau
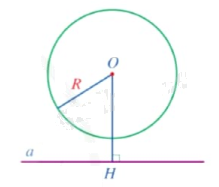
Khi đường thẳng và đường tròn không có điểm chung, ta nói đường thẳng và đường tròn không giao nhau. |
Nhận xét: Đường thẳng a và đường tròn (O;R) không giao nhau khi khoảng cách từ tâm O đến đường thẳng a lớn hơn R và ngược lại.
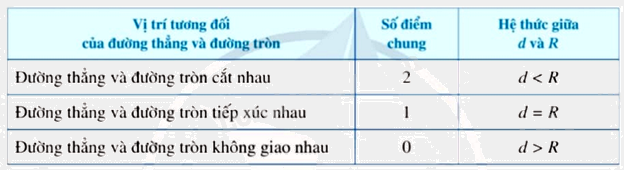
Nhận xét: Ta có thể nhận biết vị trí tương đối của đường thẳng a và đường tròn (O;R) thông qua hệ thức giữa khoảng cách d từ tâm O đến đường thẳng a và bán kính R được tóm tắt trong bảng sau:
Trong hình học phẳng, việc xác định vị trí tương đối giữa đường thẳng và đường tròn là một vấn đề cơ bản và quan trọng. Nó là nền tảng để giải quyết nhiều bài toán liên quan đến đường tròn và đường thẳng, cũng như để hiểu sâu hơn về các tính chất hình học.
Trước khi đi vào lý thuyết, chúng ta cần nắm vững một số khái niệm cơ bản:
Có ba trường hợp vị trí tương đối giữa một đường thẳng và một đường tròn:
Để xác định vị trí tương đối giữa đường thẳng và đường tròn, ta thực hiện các bước sau:
Ví dụ 1: Cho đường tròn (C) có tâm O(0,0) và bán kính r = 5. Đường thẳng d có phương trình x + y - 7 = 0. Xác định vị trí tương đối giữa đường thẳng d và đường tròn (C).
Giải:
Khoảng cách từ O(0,0) đến đường thẳng d: x + y - 7 = 0 là:
d = |1*0 + 1*0 - 7| / √(12 + 12) = 7 / √2 ≈ 4.95
Vì d < r (4.95 < 5), nên đường thẳng d cắt đường tròn (C).
Ví dụ 2: Cho đường tròn (C) có tâm O(2,1) và bán kính r = 3. Đường thẳng d có phương trình 3x - 4y + 2 = 0. Xác định vị trí tương đối giữa đường thẳng d và đường tròn (C).
Giải:
Khoảng cách từ O(2,1) đến đường thẳng d: 3x - 4y + 2 = 0 là:
d = |3*2 - 4*1 + 2| / √(32 + (-4)2) = |6 - 4 + 2| / √25 = 4 / 5 = 0.8
Vì d < r (0.8 < 3), nên đường thẳng d cắt đường tròn (C).
Để củng cố kiến thức, bạn có thể tự giải các bài tập sau:
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về lý thuyết vị trí tương đối của đường thẳng và đường tròn trong chương trình Toán 9 Cánh diều. Chúc bạn học tốt!