Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn giải quyết các bài tập trong mục 2 trang 102 sách giáo khoa Toán 9 tập 1 - Cánh diều.
Chúng tôi cam kết cung cấp nội dung chính xác, đầy đủ và giúp bạn nắm vững kiến thức Toán học một cách hiệu quả.
Trong bức ảnh ở Hình 22, sợi dây dưới cùng và bánh xe gợi nên hình ảnh đường thẳng và đường tròn tiếp xúc nhau. Theo em, đường thẳng và đường tròn đó có bao nhiêu điểm chung?
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 102 SGK Toán 9 Cánh diều
Cho tam giác \(ABC\) vuông tại \(A,AB = 3cm,BC = 5cm\). Đường thẳng \(AB\) có tiếp xúc với đường tròn \(\left( {C;4cm} \right)\) hay không? Vì sao?
Phương pháp giải:
Dựa vào kiến thức vừa học để chứng minh.
Lời giải chi tiết:
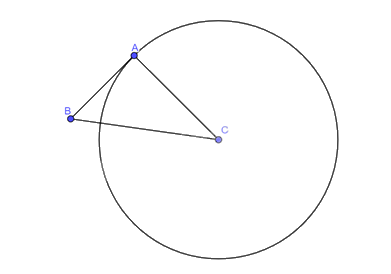
Xét tam giác \(ABC\) vuông tại \(A\), áp dụng định lí Pythagore ta có:
\(A{B^2} + A{C^2} = B{C^2} \Rightarrow {3^2} + A{C^2} = {5^2} \Rightarrow AC = 4\left( {cm} \right)\).
Vậy đường thẳng \(AB\) có tiếp xúc với đường tròn \(\left( {C;4cm} \right)\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 102 SGK Toán 9 Cánh diều
Trong bức ảnh ở Hình 22, sợi dây dưới cùng và bánh xe gợi nên hình ảnh đường thẳng và đường tròn tiếp xúc nhau. Theo em, đường thẳng và đường tròn đó có bao nhiêu điểm chung?

Phương pháp giải:
Dựa vào quan sát trực quan để đưa ra nhận xét.
Lời giải chi tiết:
Đường thẳng và đường tròn tiếp xúc nhau có 1 điểm chung.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 102 SGK Toán 9 Cánh diều
Trong bức ảnh ở Hình 22, sợi dây dưới cùng và bánh xe gợi nên hình ảnh đường thẳng và đường tròn tiếp xúc nhau. Theo em, đường thẳng và đường tròn đó có bao nhiêu điểm chung?

Phương pháp giải:
Dựa vào quan sát trực quan để đưa ra nhận xét.
Lời giải chi tiết:
Đường thẳng và đường tròn tiếp xúc nhau có 1 điểm chung.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 102 SGK Toán 9 Cánh diều
Cho tam giác \(ABC\) vuông tại \(A,AB = 3cm,BC = 5cm\). Đường thẳng \(AB\) có tiếp xúc với đường tròn \(\left( {C;4cm} \right)\) hay không? Vì sao?
Phương pháp giải:
Dựa vào kiến thức vừa học để chứng minh.
Lời giải chi tiết:
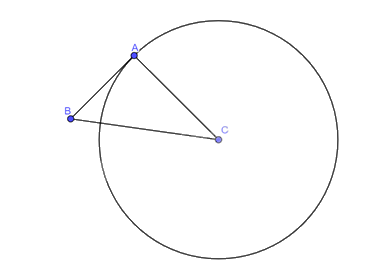
Xét tam giác \(ABC\) vuông tại \(A\), áp dụng định lí Pythagore ta có:
\(A{B^2} + A{C^2} = B{C^2} \Rightarrow {3^2} + A{C^2} = {5^2} \Rightarrow AC = 4\left( {cm} \right)\).
Vậy đường thẳng \(AB\) có tiếp xúc với đường tròn \(\left( {C;4cm} \right)\).
Mục 2 của chương trình Toán 9 tập 1 - Cánh diều tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc nhất. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Mục 2 trang 102 SGK Toán 9 tập 1 - Cánh diều bao gồm các bài tập sau:
Để xác định hệ số a của hàm số y = ax + b khi biết đồ thị của hàm số đi qua hai điểm A(x1; y1) và B(x2; y2), ta thực hiện các bước sau:
Ví dụ: Cho hàm số y = ax + 2 và đồ thị của hàm số đi qua điểm A(1; 3). Tìm giá trị của a.
Giải:
Thay tọa độ của điểm A vào phương trình y = ax + 2, ta được: 3 = a * 1 + 2 => a = 1.
Để tìm giá trị của x để hàm số y = ax + b nhận giá trị bằng 0, ta thực hiện các bước sau:
Ví dụ: Cho hàm số y = 2x - 4. Tìm giá trị của x để y = 0.
Giải:
Cho y = 0, ta có phương trình: 2x - 4 = 0 => x = 2.
Các bài toán ứng dụng thường yêu cầu học sinh xây dựng mô hình toán học dựa trên các thông tin được cung cấp trong bài toán. Sau khi xây dựng được mô hình, ta sử dụng các kiến thức về hàm số bậc nhất để giải quyết bài toán.
Ví dụ: Một người đi xe máy với vận tốc 40 km/h. Hỏi sau 2 giờ người đó đi được bao nhiêu km?
Giải:
Gọi x là thời gian đi (giờ) và y là quãng đường đi được (km). Ta có hàm số y = 40x. Khi x = 2, ta có y = 40 * 2 = 80.
Vậy sau 2 giờ người đó đi được 80 km.
Để lập bảng giá trị của hàm số y = ax + b, ta chọn một số giá trị của x và tính giá trị tương ứng của y. Sau đó, ta vẽ đồ thị của hàm số bằng cách đánh dấu các điểm (x; y) lên mặt phẳng tọa độ và nối chúng lại với nhau.
Ví dụ: Lập bảng giá trị và vẽ đồ thị của hàm số y = x + 1.
| x | y |
|---|---|
| -2 | -1 |
| -1 | 0 |
| 0 | 1 |
| 1 | 2 |
Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải quyết các bài tập trong mục 2 trang 102 SGK Toán 9 tập 1 - Cánh diều. Chúc bạn học tập tốt!