Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn giải bài tập 5 trang 66 SGK Toán 9 tập 1 - Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp tối ưu, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
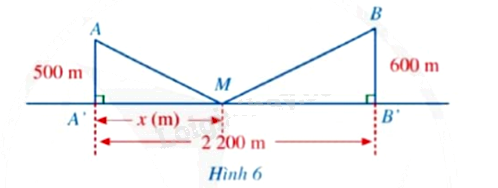
Có hai xã A, B cùng ở một bên bờ sông Lam, khoảng cách từ hai xác đó đến bờ sông lần lượt là (AA' = 500m,BB' = 600m) và người ta đo dược (A'B' = 2200m). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Giả sử vị trí của trạm cung cấp nước sạch đó là điểm M trên đoạn (A'B') với (MA' = xleft( m right)), (0 < x < 2200) (minh họa ở Hình 6). a. Hãy tính tổng khoảng cách (MA + MB) theo (x). b. Tính tổng khoảng cách (MA + MB) khi (x = 1200)
Đề bài
Có hai xã A, B cùng ở một bên bờ sông Lam, khoảng cách từ hai xác đó đến bờ sông lần lượt là \(AA' = 500m,BB' = 600m\) và người ta đo dược \(A'B' = 2200m\). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Giả sử vị trí của trạm cung cấp nước sạch đó là điểm M trên đoạn \(A'B'\) với \(MA' = x\left( m \right)\), \(0 < x < 2200\) (minh họa ở Hình 6).
a. Hãy tính tổng khoảng cách \(MA + MB\) theo \(x\).
b. Tính tổng khoảng cách \(MA + MB\) khi \(x = 1200\) (làm tròn kết quả đến hàng đơn vị của mét).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng định lí Py – ta – go và căn thức đế tính.
Lời giải chi tiết
a. Ta có: \(MB = 2200 - x\)
Áp dụng định lý Py – ta – go vào tam giác MAA’ ta có:
\(\begin{array}{l}M{A^2} = MA{'^2} + AA{'^2}\\M{A^2} = {x^2} + {500^2}\\MA = \sqrt {{x^2} + {{500}^2}} \end{array}\)
Áp dụng định lý Py – ta – go vào tam giác \(MBB'\) ta có:
\(\begin{array}{l}M{B^2} = BB{'^2} + MB{'^2} \Rightarrow M{B^2} = {600^2} + {\left( {2200 - x} \right)^2}\\MB = \sqrt {{600^2} + {\left( {2200 - x} \right)^2}} \end{array}\)
Vậy \(MA + MB = \sqrt {{x^2} + {{500}^2}} + \sqrt {{600^2} + {\left( {2200 - x} \right)^2}}. \)
b. Thay \(x = 1200\) vào biểu thức tính \(MA + MB\), ta được:
\(MA + MB = \sqrt {{{1200}^2} + {{500}^2}} + \sqrt {{600^2} + {\left( {2200 - 1200} \right)^2}} \\ = \sqrt {1440000 + 250000} + \sqrt {{600^2} + {1000^2}} \\ = \sqrt {1690000} + \sqrt {1360000} \\MA + MB \approx 2466\left( m \right).\)
Bài tập 5 trang 66 SGK Toán 9 tập 1 - Cánh diều thuộc chương trình đại số, tập trung vào việc giải phương trình bậc hai một ẩn. Để giải quyết bài tập này, học sinh cần nắm vững các kiến thức cơ bản về phương trình bậc hai, bao gồm:
Bài tập 5 thường bao gồm các phương trình bậc hai với các hệ số khác nhau. Yêu cầu của bài tập là tìm nghiệm của phương trình hoặc xác định số nghiệm của phương trình dựa vào dấu của delta (Δ).
Để giúp các em học sinh hiểu rõ hơn, chúng ta sẽ cùng nhau giải chi tiết từng câu của bài tập 5:
Phương trình: 2x2 - 5x + 2 = 0
Bước 1: Xác định các hệ số a, b, c: a = 2, b = -5, c = 2
Bước 2: Tính delta (Δ): Δ = (-5)2 - 4 * 2 * 2 = 25 - 16 = 9
Bước 3: Xác định số nghiệm: Vì Δ > 0, phương trình có hai nghiệm phân biệt.
Bước 4: Tính nghiệm:
x1 = (5 + √9) / (2 * 2) = (5 + 3) / 4 = 2
x2 = (5 - √9) / (2 * 2) = (5 - 3) / 4 = 1/2
Vậy, nghiệm của phương trình là x1 = 2 và x2 = 1/2.
Phương trình: x2 - 4x + 4 = 0
Bước 1: Xác định các hệ số a, b, c: a = 1, b = -4, c = 4
Bước 2: Tính delta (Δ): Δ = (-4)2 - 4 * 1 * 4 = 16 - 16 = 0
Bước 3: Xác định số nghiệm: Vì Δ = 0, phương trình có nghiệm kép.
Bước 4: Tính nghiệm:
x = -b / (2a) = -(-4) / (2 * 1) = 2
Vậy, nghiệm kép của phương trình là x = 2.
Phương trình: 3x2 + 2x + 1 = 0
Bước 1: Xác định các hệ số a, b, c: a = 3, b = 2, c = 1
Bước 2: Tính delta (Δ): Δ = (2)2 - 4 * 3 * 1 = 4 - 12 = -8
Bước 3: Xác định số nghiệm: Vì Δ < 0, phương trình vô nghiệm.
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Hy vọng với hướng dẫn chi tiết này, các em học sinh đã có thể tự tin giải bài tập 5 trang 66 SGK Toán 9 tập 1 - Cánh diều. Chúc các em học tập tốt!