Chào mừng bạn đến với bài học lý thuyết về một số hệ thức quan trọng liên quan đến cạnh và góc trong tam giác vuông, chương trình Toán 9 Cánh diều. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng vững chắc để giải quyết các bài toán liên quan đến tam giác vuông một cách hiệu quả.
Chúng ta sẽ cùng nhau khám phá các định nghĩa, định lý và công thức cần thiết, đồng thời luyện tập thông qua các ví dụ minh họa cụ thể. Mục tiêu là giúp bạn hiểu rõ bản chất của các hệ thức và áp dụng chúng một cách linh hoạt trong quá trình học tập và làm bài tập.
1. Tính cạnh góc vuông theo cạnh huyền và tỉ số lượng giác của góc nhọn Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề. Cạnh góc vuông = (cạnh huyền ) × (sin góc đối) = (cạnh huyền ) × (cosin góc kề)
1. Tính cạnh góc vuông theo cạnh huyền và tỉ số lượng giác của góc nhọn
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề. Cạnh góc vuông = (cạnh huyền ) × (sin góc đối) = (cạnh huyền ) × (cosin góc kề) |
Ví dụ 1:
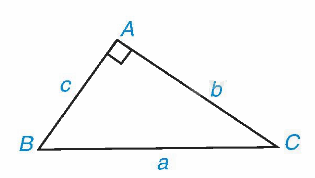
Trong tam giác ABC vuông tại A, ta có:
\(\begin{array}{l}b = a.\sin B = a.\cos C;\\c = a.\sin C = a.\cos B.\end{array}\)
2. Tính cạnh góc vuông theo cạnh góc vuông còn lại và tỉ số lượng giác của góc nhọn
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tang góc đối hoặc côtang góc kề. Cạnh góc vuông = (cạnh góc vuông còn lại ) × (tan góc đối) = (cạnh góc vuông còn lại ) × (cot góc kề) |
Ví dụ 2:
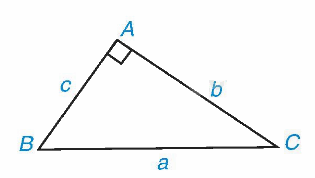
Trong tam giác ABC vuông tại A, ta có:
\(\begin{array}{l}b = c.\tan B = c.\cot C;\\c = b.\tan C = b.\cot B.\end{array}\)
3. Áp dụng tỉ số lượng giác của góc nhọn để giải tam giác vuông
Giải tam giác vuông là tìm tất cả độ dài các cạnh và số đo các góc còn lại của tam giác đó.
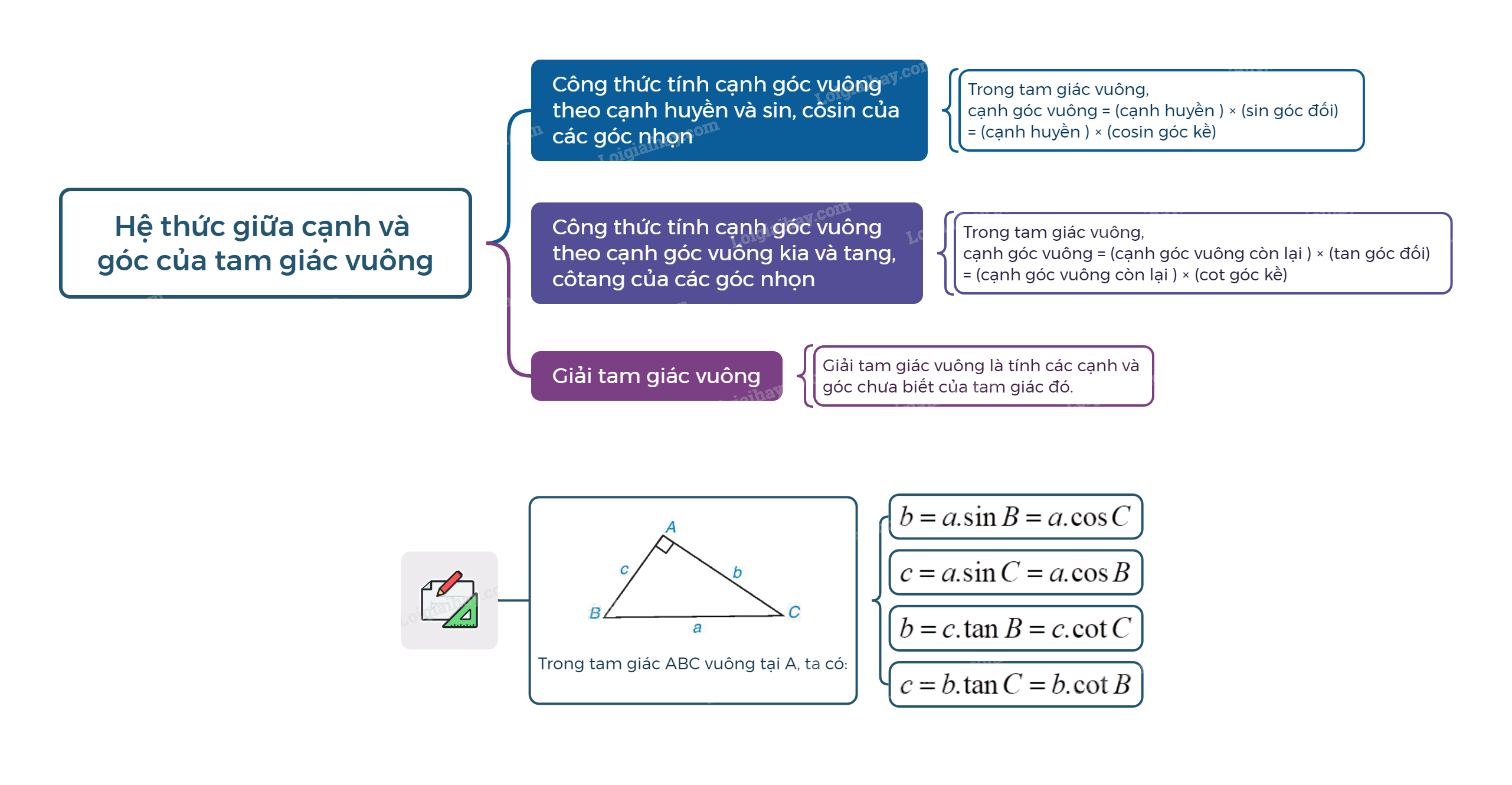
Tam giác vuông là một trong những hình cơ bản và quan trọng trong hình học. Việc nắm vững các hệ thức về cạnh và góc trong tam giác vuông là nền tảng để giải quyết nhiều bài toán thực tế và nâng cao kiến thức toán học.
Tam giác vuông là tam giác có một góc bằng 90 độ. Cạnh đối diện với góc vuông được gọi là cạnh huyền, hai cạnh còn lại được gọi là cạnh góc vuông.
Trong một tam giác vuông, tỉ số giữa các cạnh được gọi là tỉ số lượng giác. Các tỉ số lượng giác cơ bản bao gồm:
Trong đó α là góc nhọn trong tam giác vuông.
Các hệ thức lượng trong tam giác vuông liên hệ giữa các cạnh và góc của tam giác vuông.
Ví dụ 1: Cho tam giác ABC vuông tại A, AB = 3cm, AC = 4cm. Tính BC và sin B, cos B, tan B.
Giải:
Ví dụ 2: Cho tam giác ABC vuông tại A, đường cao AH = 2cm, BH = 1cm. Tính CH.
Giải:
Áp dụng hệ thức giữa đường cao và các đoạn thẳng trên cạnh huyền: AH2 = BH * CH => 22 = 1 * CH => CH = 4cm.
Để củng cố kiến thức, bạn hãy tự giải các bài tập sau:
Hy vọng bài học này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết một số hệ thức về cạnh và góc trong tam giác vuông Toán 9 Cánh diều. Chúc bạn học tập tốt!