Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 2 trang 51 sách giáo khoa Toán 9 tập 2 của nhà xuất bản Cánh diều.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải một cách cẩn thận, kèm theo các bước giải chi tiết và giải thích rõ ràng để giúp bạn nắm vững kiến thức.
Cho hàm số (y = frac{1}{3}{x^2}). a) Tìm giá trị của y tương ứng với giái trị của x trong bảng sau: b) Dựa vào bảng giá trị trên, vẽ đồ thị của hàm số đó. c) Tìm những điểm thuộc đồ thị của hàm số có hoành độ lần lượt bằng -6; 10. d) Tìm những điểm thuộc đồ thị của hàm số có tung độ bằng 27.
Đề bài
Cho hàm số \(y = \frac{1}{3}{x^2}\).
a) Tìm giá trị của y tương ứng với giái trị của x trong bảng sau:

b) Dựa vào bảng giá trị trên, vẽ đồ thị của hàm số đó.
c) Tìm những điểm thuộc đồ thị của hàm số có hoành độ lần lượt bằng -6; 10.
d) Tìm những điểm thuộc đồ thị của hàm số có tung độ bằng 27.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Thay từng giá trị của x vào hàm số \(y = \frac{1}{3}{x^2}\) để tìm được y tương ứng.
b) Dựa vào bảng giá trị để vẽ đồ thị.
c) Thay lần lượt \(x = - 6,x = 10\) vào hàm số để tìm được tung độ tương ứng.
d) Thay \(y = 27\) hàm số để tìm được các hoành độ tương ứng.
Lời giải chi tiết
a) Ta có bảng giá trị sau:

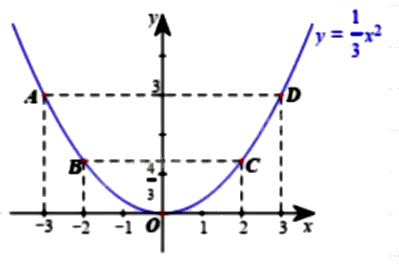
b) Đồ thị hàm số \(y = \frac{1}{3}{x^2} \) là một parabol đi qua các điểm \(A(-3;3); B(-2;\frac{4}{3}); O(0;0); C(2;\frac{4}{3}); D(3;3)\)
c) Thay \(x = - 6\) vào hàm số \(y = \frac{1}{3}{x^2}\) ta được:
\(y = \frac{1}{3}{( - 6)^2} \Leftrightarrow y = 12\).
Ta có điểm (-6; 12) thuộc đồ thị hàm số \(y = \frac{1}{3}{x^2}\).
Thay \(x = 10\) vào hàm số \(y = \frac{1}{3}{x^2}\) ta được:
\(y = \frac{1}{3}{(10)^2} \Leftrightarrow y = \frac{{100}}{3}\).
Ta có điểm \(\left( {10;\frac{{100}}{3}} \right)\) thuộc đồ thị hàm số \(y = \frac{1}{3}{x^2}\).
d) Thay \(y = 27\) vào hàm số \(y = \frac{1}{3}{x^2}\) ta được:
\(27 = \frac{1}{3}{x^2} \Leftrightarrow {x^2} = 81 \Leftrightarrow x = \pm 9\).
Ta có điểm \(\left( { - 9;27} \right),\left( {9;27} \right)\) thuộc đồ thị hàm số \(y = \frac{1}{3}{x^2}\).
Bài tập 2 trang 51 SGK Toán 9 tập 2 - Cánh diều thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để xác định hệ số góc và đường thẳng song song, vuông góc.
Bài tập 2 bao gồm các câu hỏi nhỏ, yêu cầu học sinh:
Đường thẳng có dạng y = ax + b. Hệ số góc của đường thẳng là a. Để xác định a, ta cần biết tọa độ của hai điểm thuộc đường thẳng hoặc một điểm và góc nghiêng của đường thẳng.
Ví dụ: Nếu đường thẳng đi qua hai điểm A(x1, y1) và B(x2, y2), thì hệ số góc a được tính bằng công thức: a = (y2 - y1) / (x2 - x1).
Hai đường thẳng y = a1x + b1 và y = a2x + b2 song song khi và chỉ khi a1 = a2 và b1 ≠ b2.
Điều này có nghĩa là hai đường thẳng có cùng hệ số góc nhưng khác tung độ gốc.
Hai đường thẳng y = a1x + b1 và y = a2x + b2 vuông góc khi và chỉ khi a1 * a2 = -1.
Điều này có nghĩa là tích của hệ số góc của hai đường thẳng bằng -1.
Để viết phương trình đường thẳng đi qua điểm M(x0, y0) và có hệ số góc a, ta sử dụng công thức: y - y0 = a(x - x0).
Ví dụ: Đường thẳng đi qua điểm M(1, 2) và có hệ số góc a = 3 có phương trình: y - 2 = 3(x - 1) hay y = 3x - 1.
Hàm số bậc nhất có dạng y = ax + b, trong đó a là hệ số góc và b là tung độ gốc.
Hệ số góc a quyết định độ dốc của đường thẳng. Nếu a > 0, đường thẳng đi lên từ trái sang phải. Nếu a < 0, đường thẳng đi xuống từ trái sang phải. Nếu a = 0, đường thẳng là đường thẳng ngang.
Tung độ gốc b là tọa độ giao điểm của đường thẳng với trục Oy.
Hy vọng bài giải bài tập 2 trang 51 SGK Toán 9 tập 2 - Cánh diều này đã giúp bạn hiểu rõ hơn về hàm số bậc nhất và các ứng dụng của nó. Hãy luyện tập thêm các bài tập khác để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.