Chào mừng bạn đến với bài học lý thuyết về một số phép biến đổi căn thức bậc hai trong chương trình Toán 9 Cánh diều. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng và các quy tắc quan trọng để giải quyết các bài toán liên quan đến căn thức một cách hiệu quả.
Chúng ta sẽ cùng nhau khám phá các khái niệm cơ bản, các tính chất của căn thức bậc hai, và các phép biến đổi thường gặp. Mục tiêu là giúp bạn hiểu rõ bản chất của vấn đề và áp dụng linh hoạt vào các bài tập thực tế.
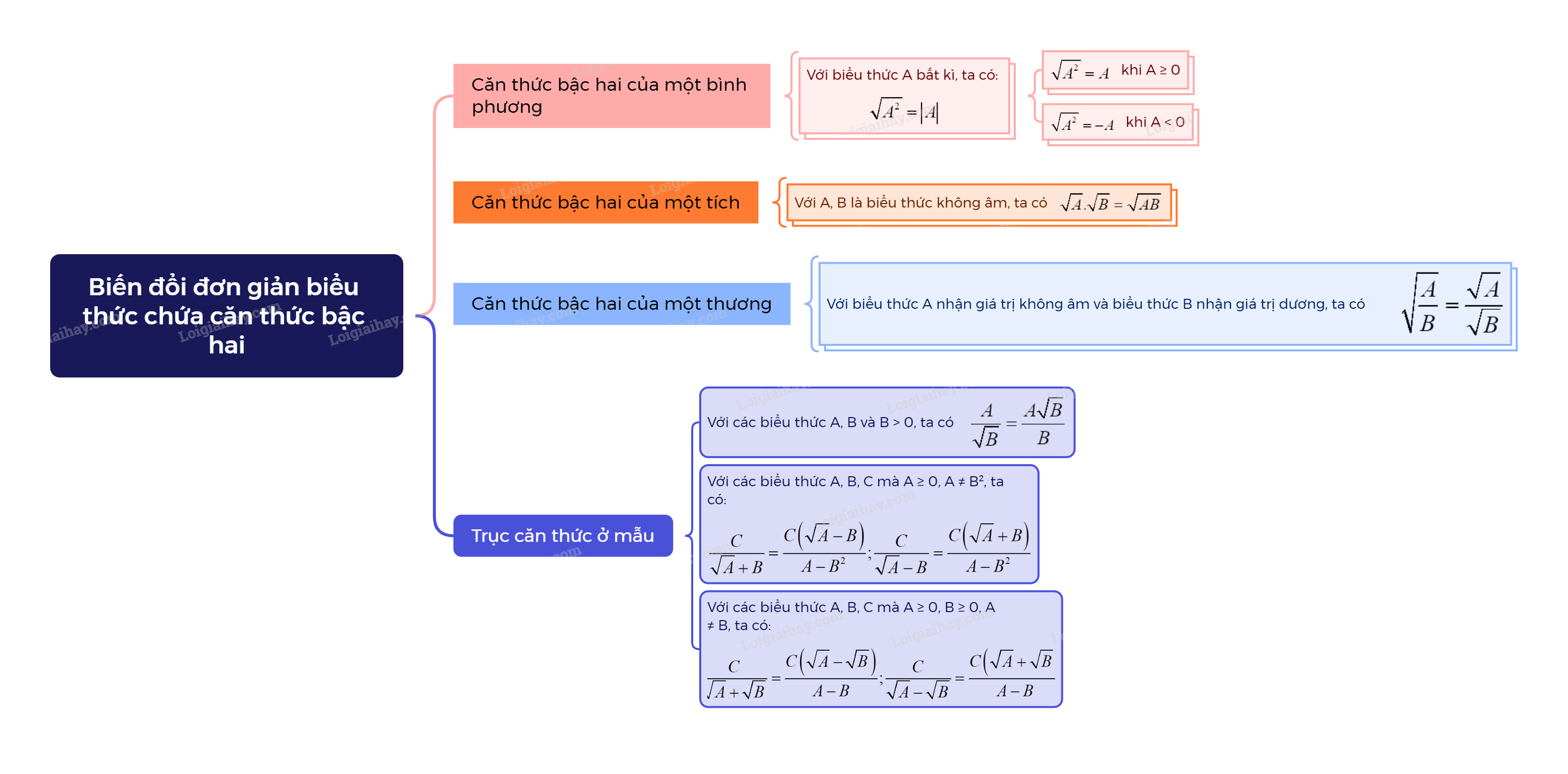
1. Căn thức bậc hai của một bình phương Quy tắc về căn thức bậc hai của một bình phương: Với mỗi biểu thức A, ta có: (sqrt {{A^2}} = left| A right|), tức là: (sqrt {{A^2}} = left| A right| = left{ begin{array}{l}A,khi,A ge 0\ - A,khi,A < 0end{array} right.)
1. Căn thức bậc hai của một bình phương
Quy tắc về căn thức bậc hai của một bình phương:
Với mỗi biểu thức A, ta có: \(\sqrt {{A^2}} = \left| A \right|\), tức là: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,khi\,A \ge 0\\ - A\,khi\,A < 0\end{array} \right.\) |
Ví dụ:\(\sqrt {{{\left( {x - 2} \right)}^2}} = \left| {x - 2} \right| = \left\{ \begin{array}{l}x - 2\,khi\,x \ge 2\\2 - x\,khi\,x \le 2\end{array} \right.\)
2. Căn thức bậc hai của một tích
Quy tắc về căn thức bậc hai của một tích:
Với các biểu thức A, B không âm, ta có: \(\sqrt {A.B} = \sqrt A .\sqrt B \). |
Ví dụ:
\(\sqrt {4{a^2}} = \sqrt 4 .\sqrt {{a^2}} = 2\left| a \right|\);
\(\sqrt {2a} .\sqrt {8a} = \sqrt {2a.8a} = \sqrt {16{a^2}} = \sqrt {16} .\sqrt {{a^2}} = 4\left| a \right|\).
3. Căn thức bậc hai của một thương
Quy tắc về căn bậc hai của một thương
Với các biểu thức A không âm và biểu thức B dương, ta có: \(\sqrt {\frac{A}{B}} = \frac{{\sqrt A }}{{\sqrt B }}\). |
Ví dụ:
\(\sqrt {\frac{{4{a^2}}}{{25}}} = \frac{{\sqrt {4{a^2}} }}{{\sqrt {25} }} = \frac{{2\left| a \right|}}{5}\);
\(\frac{{\sqrt {125a} }}{{\sqrt {5a} }} = \sqrt {\frac{{125a}}{{5a}}} = \sqrt {25} = 5\).
4. Trục căn thức ở mẫu
Nhận xét: Phép biến đổi làm mất căn thức bậc hai ở mẫu thức của một biểu thức được gọi là trục căn thức ở mẫu của biểu thức đó.
- Với các biểu thức A, B và B > 0, ta có \(\frac{A}{{\sqrt B }} = \frac{{A\sqrt B }}{B}\). - Với các biểu thức A, B, C mà \(B \ge 0,{A^2} \ne B\), ta có: \(\frac{C}{{A + \sqrt B }} = \frac{{C\left( {A - \sqrt B } \right)}}{{{A^2} - B}};\frac{C}{{A - \sqrt B }} = \frac{{C\left( {A + \sqrt B } \right)}}{{{A^2} - B}}\). (\(A - \sqrt B \) được gọi là biểu thức liên hợp của \(A + \sqrt B \) và ngược lại). - Với các biểu thức A, B, C mà \(A \ge 0,B \ge 0,A \ne B\), ta có: \(\frac{C}{{\sqrt A + \sqrt B }} = \frac{{C\left( {\sqrt A - \sqrt B } \right)}}{{A - B}};\frac{C}{{\sqrt A - \sqrt B }} = \frac{{C\left( {\sqrt A + \sqrt B } \right)}}{{A - B}}\). (\(\sqrt A - \sqrt B \) được gọi là biểu thức liên hợp của \(\sqrt A + \sqrt B \) và ngược lại). |
Ví dụ:
\(\frac{2}{{3\sqrt 5 }} = \frac{{2\sqrt 5 }}{{3{{\left( {\sqrt 5 } \right)}^2}}} = \frac{{2\sqrt 5 }}{{3.5}} = \frac{{2\sqrt 5 }}{{15}}\);
\(\frac{a}{{3 - 2\sqrt 2 }} = \frac{{a\left( {3 + 2\sqrt 2 } \right)}}{{\left( {3 - 2\sqrt 2 } \right).\left( {3 + 2\sqrt 2 } \right)}} = \frac{{a\left( {3 + 2\sqrt 2 } \right)}}{{{3^2} - {{\left( {2\sqrt 2 } \right)}^2}}} = \frac{{a\left( {3 + 2\sqrt 2 } \right)}}{{9 - 8}} = \left( {3 + 2\sqrt 2 } \right)a\).
Căn thức bậc hai là một khái niệm quan trọng trong đại số, đặc biệt là ở chương trình Toán 9. Việc nắm vững lý thuyết và các phép biến đổi liên quan đến căn thức bậc hai là nền tảng để giải quyết nhiều bài toán phức tạp hơn trong tương lai. Bài viết này sẽ trình bày chi tiết lý thuyết về một số phép biến đổi căn thức bậc hai của biểu thức đại số, theo chương trình Toán 9 Cánh diều.
Căn thức bậc hai của một số a (với a ≥ 0) là số x sao cho x2 = a. Ký hiệu: √a. Trong đó:
Ví dụ: √9 = 3 vì 32 = 9.
Căn thức bậc hai √A chỉ xác định khi và chỉ khi A ≥ 0.
Ví dụ: Căn thức √x + 1 xác định khi và chỉ khi x + 1 ≥ 0, tức là x ≥ -1.
Ví dụ 1: Rút gọn biểu thức √(18). Ta có:
√(18) = √(9 * 2) = √9 * √2 = 3√2
Ví dụ 2: Đưa thừa số vào trong dấu căn: 2√3. Ta có:
2√3 = √(22 * 3) = √12
Ví dụ 3: Khử mẫu của căn thức: √(2/3). Ta có:
√(2/3) = √2/√3 = (√2 * √3) / (√3 * √3) = √6/3
Hãy tự luyện tập với các bài tập sau để củng cố kiến thức:
Lý thuyết về một số phép biến đổi căn thức bậc hai của biểu thức đại số Toán 9 Cánh diều là một phần quan trọng trong chương trình học. Việc nắm vững các khái niệm, điều kiện xác định, các phép biến đổi và tính chất của căn thức bậc hai sẽ giúp bạn giải quyết các bài toán một cách hiệu quả và chính xác. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.