Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 82, 83 SGK Toán 9 tập 1 - Cánh diều trên giaitoan.edu.vn. Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi luôn cố gắng mang đến những bài giải chất lượng nhất, đáp ứng nhu cầu học tập của các em.
Cho tam giác (ABC) vuông tại (A) (Hình 13). a) Biểu diễn (sin B,cos C) theo (AC,BC). b) Viết công thức tính (AC) theo (BC) và (sin B). c) Viết công thức tính (AC) theo (BC) và (cos C).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 82SGK Toán 9 Cánh diều
Cho tam giác \(ABC\) vuông tại \(A\) (Hình 13).
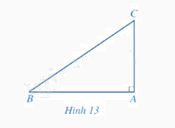
a) Biểu diễn \(\sin B,\cos C\) theo \(AC,BC\).
b) Viết công thức tính \(AC\) theo \(BC\) và \(\sin B\).
c) Viết công thức tính \(AC\) theo \(BC\) và \(\cos C\).
Phương pháp giải:
Dựa vào định nghĩa tỉ số lượng giác để giải bài toán.
Lời giải chi tiết:
a) \(\sin B = \frac{{AC}}{{BC}}\);\(\cos C = \frac{{AC}}{{BC}}\).
b) \(AC = BC.\sin B\).
c) \(AC = BC.\cos C\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 83SGK Toán 9 Cánh diều
Cho tam giác nhọn \(ABC\) có đường cao \(CK\). Biểu thị \(CK\) theo \(AC\) và \(\sin A\). Từ đó, chứng minh diện tích tam giác \(ABC\) bằng \(\frac{1}{2}.AB.AC.\sin A\).
Phương pháp giải:
Dựa vào định nghĩ tỉ số lượng giác kết hợp với mối quan hệ giữa cạnh góc vuông, cạnh huyền và tỉ số lượng giác để giải bài toán.
Lời giải chi tiết:
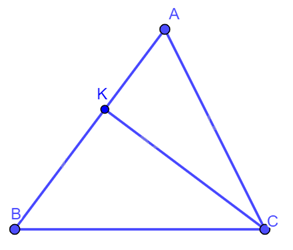
Vì tam giác \(ACK\) vuông tại \(K\) nên: \(CK = AC.\sin A\).
Ta có: \({S_{ABC}} = \frac{1}{2}CK.AB = \frac{1}{2}.AB.AC.\sin A\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 82SGK Toán 9 Cánh diều
Cho tam giác \(ABC\) vuông tại \(A\) (Hình 13).
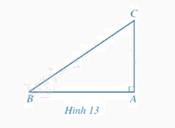
a) Biểu diễn \(\sin B,\cos C\) theo \(AC,BC\).
b) Viết công thức tính \(AC\) theo \(BC\) và \(\sin B\).
c) Viết công thức tính \(AC\) theo \(BC\) và \(\cos C\).
Phương pháp giải:
Dựa vào định nghĩa tỉ số lượng giác để giải bài toán.
Lời giải chi tiết:
a) \(\sin B = \frac{{AC}}{{BC}}\);\(\cos C = \frac{{AC}}{{BC}}\).
b) \(AC = BC.\sin B\).
c) \(AC = BC.\cos C\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 83SGK Toán 9 Cánh diều
Tính độ cao \(AC\) trong Hình 12 khi \(BC = 20m\) (làm tròn kết quả đến hàng phần mười của mét)

Phương pháp giải:
Dựa vào quan hệ giữa cạnh huyền và tỉ số lượng giác của góc nhọn để tính.
Lời giải chi tiết:
Độ cao AC là:
\(AC = BC.\sin 15^\circ = 20.\sin 15^\circ \approx 5,2\left( m \right)\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 2 trang 83SGK Toán 9 Cánh diều
Cho tam giác nhọn \(ABC\) có đường cao \(CK\). Biểu thị \(CK\) theo \(AC\) và \(\sin A\). Từ đó, chứng minh diện tích tam giác \(ABC\) bằng \(\frac{1}{2}.AB.AC.\sin A\).
Phương pháp giải:
Dựa vào định nghĩ tỉ số lượng giác kết hợp với mối quan hệ giữa cạnh góc vuông, cạnh huyền và tỉ số lượng giác để giải bài toán.
Lời giải chi tiết:
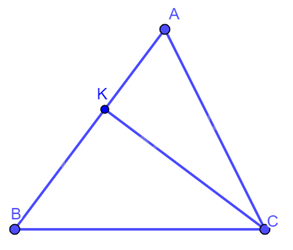
Vì tam giác \(ACK\) vuông tại \(K\) nên: \(CK = AC.\sin A\).
Ta có: \({S_{ABC}} = \frac{1}{2}CK.AB = \frac{1}{2}.AB.AC.\sin A\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 1 trang 83SGK Toán 9 Cánh diều
Tính độ cao \(AC\) trong Hình 12 khi \(BC = 20m\) (làm tròn kết quả đến hàng phần mười của mét)

Phương pháp giải:
Dựa vào quan hệ giữa cạnh huyền và tỉ số lượng giác của góc nhọn để tính.
Lời giải chi tiết:
Độ cao AC là:
\(AC = BC.\sin 15^\circ = 20.\sin 15^\circ \approx 5,2\left( m \right)\).
Mục 1 của chương trình Toán 9 tập 1 - Cánh diều tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc nhất. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 1 yêu cầu học sinh nhắc lại các khái niệm cơ bản về hàm số bậc nhất, bao gồm định nghĩa, dạng tổng quát, hệ số góc, và cách xác định hàm số.
Bài 2 tập trung vào việc vẽ đồ thị của hàm số bậc nhất. Học sinh cần nắm vững cách xác định các điểm thuộc đồ thị và cách vẽ đường thẳng đi qua các điểm đó.
Bài 3 yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế, ví dụ như tính quãng đường đi được của một vật chuyển động đều, tính tiền lương của một công nhân theo thời gian làm việc, hoặc tính giá trị của một sản phẩm theo số lượng mua.
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1 trang 82, 83 SGK Toán 9 tập 1 - Cánh diều:
| Bài tập | Lời giải |
|---|---|
| Bài 1 | (Lời giải chi tiết bài 1) |
| Bài 2 | (Lời giải chi tiết bài 2) |
| Bài 3 | (Lời giải chi tiết bài 3) |
Hy vọng rằng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn trong việc giải các bài tập mục 1 trang 82, 83 SGK Toán 9 tập 1 - Cánh diều. Chúc các em học tập tốt!