Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết mục 2 trang 84 SGK Toán 9 tập 1 - Cánh diều, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic, kèm theo các ví dụ minh họa để bạn dễ dàng theo dõi và áp dụng vào các bài tập tương tự.
Cho tam giác (ABC) vuông tại (A) (Hình 17) a) Biểu diễn (tan B,cot C) theo (AB,AC). b) Viết công thức tính (AC) theo (AB) và (tan B). c) Viết công thức tính (AC) theo (AB) và (cot C).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 84SGK Toán 9 Cánh diều
Cho tam giác \(ABC\) vuông tại \(A\) (Hình 17)
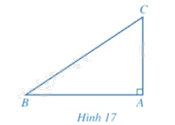
a) Biểu diễn \(\tan B,\cot C\) theo \(AB,AC\).
b) Viết công thức tính \(AC\) theo \(AB\) và \(\tan B\).
c) Viết công thức tính \(AC\) theo \(AB\) và \(\cot C\).
Phương pháp giải:
Dựa vào định nghĩa tỉ số lượng giác để giải bài toán.
Lời giải chi tiết:
a) Vì tam giác \(ABC\) vuông tại \(A\) nên:
\(\tan B = \frac{{CA}}{{AB}}\);\(\cot C = \frac{{AC}}{{AB}}\).
b) Ta có: \(AC = AB.\tan B\).
c) Ta có: \(AC = AB.\cot C\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 84 SGK Toán 9 Cánh diều
Tính \(AB\) trong Hình 17 khi \(AC = 4cm\) và \(\widehat B = 34^\circ \) (làm tròn kết quả đến hàng phần mười của centimét).
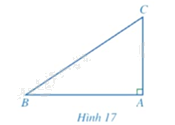
Phương pháp giải:
Dựa vào mỗi quan hệ giữa cạnh góc vuông và tỉ số lượng giác để giải bài toán.
Lời giải chi tiết:
Vì tam giác \(ABC\) vuông tại \(A\) nên:
\(AB = AC.\cot B = 4.\cot 34^\circ \approx 5,9\left( {cm} \right)\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 84SGK Toán 9 Cánh diều
Cho tam giác \(ABC\) vuông tại \(A\) (Hình 17)
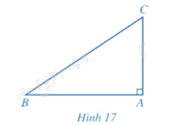
a) Biểu diễn \(\tan B,\cot C\) theo \(AB,AC\).
b) Viết công thức tính \(AC\) theo \(AB\) và \(\tan B\).
c) Viết công thức tính \(AC\) theo \(AB\) và \(\cot C\).
Phương pháp giải:
Dựa vào định nghĩa tỉ số lượng giác để giải bài toán.
Lời giải chi tiết:
a) Vì tam giác \(ABC\) vuông tại \(A\) nên:
\(\tan B = \frac{{CA}}{{AB}}\);\(\cot C = \frac{{AC}}{{AB}}\).
b) Ta có: \(AC = AB.\tan B\).
c) Ta có: \(AC = AB.\cot C\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 84 SGK Toán 9 Cánh diều
Tính \(AB\) trong Hình 17 khi \(AC = 4cm\) và \(\widehat B = 34^\circ \) (làm tròn kết quả đến hàng phần mười của centimét).
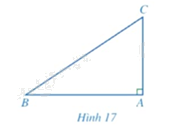
Phương pháp giải:
Dựa vào mỗi quan hệ giữa cạnh góc vuông và tỉ số lượng giác để giải bài toán.
Lời giải chi tiết:
Vì tam giác \(ABC\) vuông tại \(A\) nên:
\(AB = AC.\cot B = 4.\cot 34^\circ \approx 5,9\left( {cm} \right)\).
Mục 2 trang 84 SGK Toán 9 tập 1 - Cánh diều thường xoay quanh các bài toán liên quan đến hàm số bậc nhất, bao gồm việc xác định hệ số góc, phương trình đường thẳng, và ứng dụng của hàm số trong việc giải quyết các bài toán thực tế. Để giải quyết hiệu quả các bài toán này, học sinh cần nắm vững các khái niệm cơ bản về hàm số, đặc biệt là hàm số bậc nhất.
Hàm số bậc nhất có dạng y = ax + b, trong đó a là hệ số góc và b là tung độ gốc. Hệ số góc a quyết định độ dốc của đường thẳng, và tung độ gốc b là giao điểm của đường thẳng với trục Oy.
Để giải các bài toán liên quan đến hàm số bậc nhất, học sinh có thể áp dụng các phương pháp sau:
Bài tập: Tìm phương trình đường thẳng đi qua hai điểm A(1; 2) và B(3; 4).
Lời giải:
Mục 2 trang 84 thường xuất hiện các dạng bài tập sau:
Để học tập và luyện tập hiệu quả các bài toán liên quan đến hàm số bậc nhất, bạn nên:
Giải mục 2 trang 84 SGK Toán 9 tập 1 - Cánh diều đòi hỏi học sinh phải nắm vững các khái niệm cơ bản về hàm số bậc nhất và áp dụng các phương pháp giải phù hợp. Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trong bài viết này, bạn sẽ tự tin hơn trong quá trình học tập và giải quyết các bài toán liên quan đến hàm số bậc nhất.
| Khái niệm | Giải thích |
|---|---|
| Hệ số góc | Độ dốc của đường thẳng |
| Tung độ gốc | Giao điểm của đường thẳng với trục Oy |
| Hàm số đồng biến | Đường thẳng đi lên |
| Hàm số nghịch biến | Đường thẳng đi xuống |