Chào mừng bạn đến với bài học lý thuyết Hình nón Toán 9 Cánh diều trên giaitoan.edu.vn. Bài viết này sẽ cung cấp đầy đủ kiến thức cơ bản, các định nghĩa, tính chất và công thức quan trọng liên quan đến hình nón.
Chúng tôi sẽ giúp bạn hiểu rõ về hình nón, cách tính diện tích xung quanh, diện tích toàn phần và thể tích của hình nón một cách dễ dàng và hiệu quả.
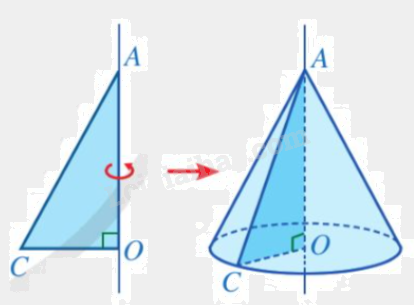
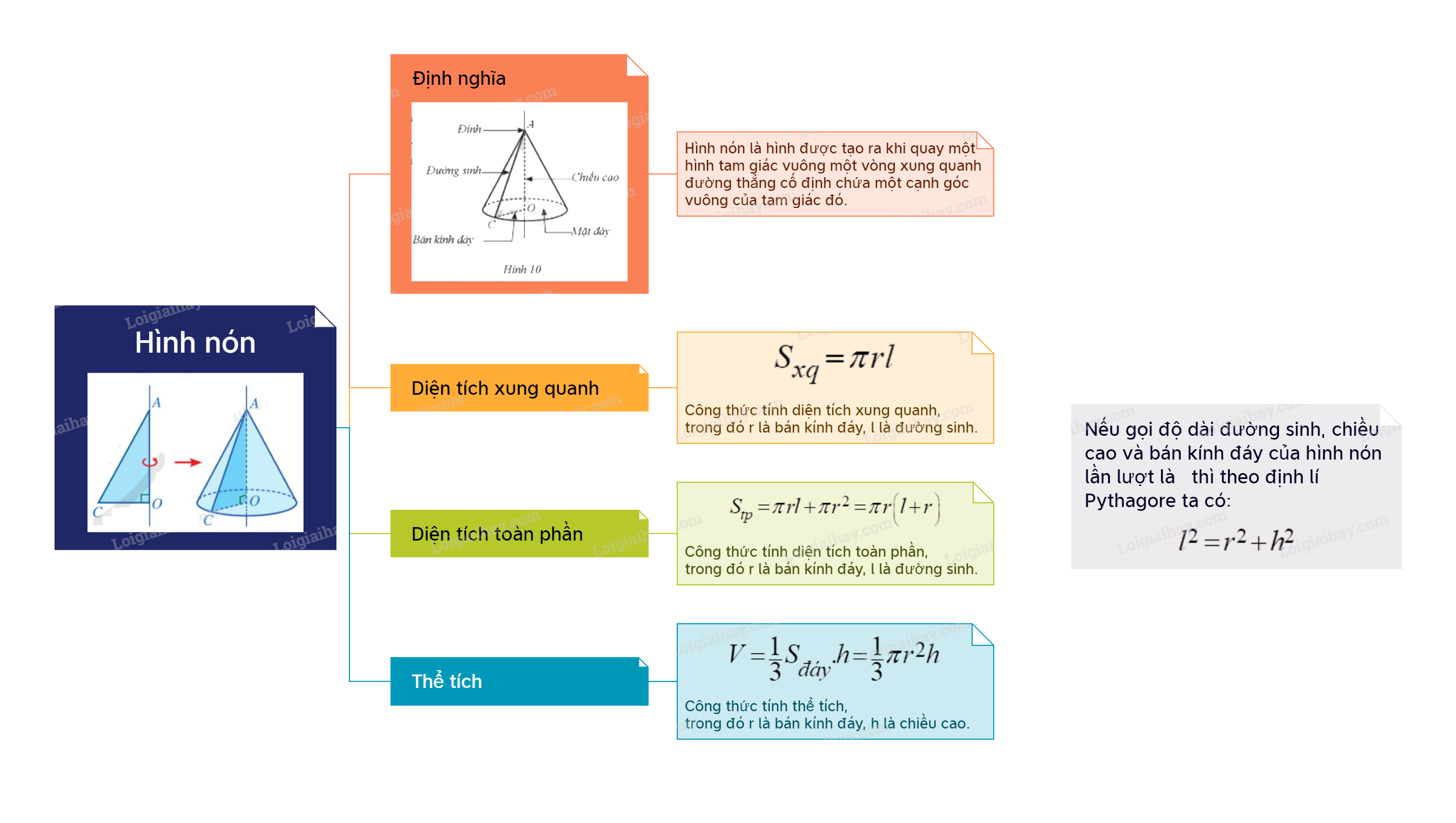
1. Hình nón Định nghĩa Hình nón là hình được tạo ra khi quay một hình tam giác vuông một vòng xung quanh đường thẳng cố định chứa một cạnh góc vuông của tam giác đó.
1. Hình nón
Định nghĩa
Hình nón là hình được tạo ra khi quay một hình tam giác vuông một vòng xung quanh đường thẳng cố định chứa một cạnh góc vuông của tam giác đó. |
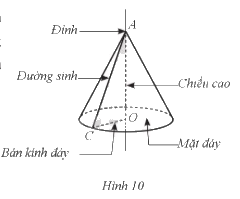
Với hình nón trên, ta có:
- Điểm A là đỉnh;
- Hình tròn tâm O bán kính OC là mặt đáy;
- Độ dài cạnh OC được gọi là bán kính đáy;
- Độ dài cạnh AO được gọi là chiều cao;
- Cạnh AC quét nên mặt xung quanh của hình nón, mỗi vị trí của cạnh AC được gọi là một đường sinh.
Chú ý: Nếu gọi độ dài đường sinh, chiều cao và bán kính đáy của hình nón lần lượt là \(l,h,r\) thì theo định lí Pythagore ta có:
\({l^2} = {r^2} + {h^2}\).
Ví dụ:
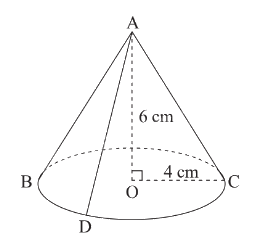
Hình nón có:
+ A là đỉnh;
+ chiều cao là 6cm;
+ bán kính đáy là 4cm.
+ các đường sinh là: AB, AC, AD.
2. Diện tích xung quanh của hình nón
Diện tích xung quanh của hình nón
Diện tích xung quanh \({S_{xq}}\) của hình nón có bán kính đáy r, độ dài đường sinh l là: \({S_{xq}} = \pi rl\). |
Diện tích toàn phần của hình nón
Diện tích toàn phần \({S_{tp}}\) của hình nón bằng tổng của diện tích xung quanh và diện tích mặt đáy của hình nón đó: \({S_{tp}} = \pi rl + \pi {r^2} = \pi r\left( {l + r} \right)\). |
Ví dụ:
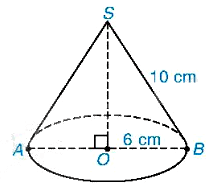
Diện tích xung quanh của hình nón là:
\({S_{xq}} = \pi rl = \pi .6.10 = 60\pi \left( {c{m^2}} \right)\).
3. Thể tích của hình nón
Thể tích V của hình nón có bán kính đáy r và chiều cao h là: \(V = \frac{1}{3}\pi {r^2}h\). |
Ví dụ:
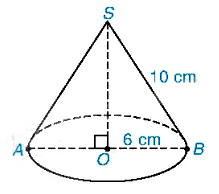
Tam giác SOB vuông tại O nên theo định lí Pythagore ta có:
\(\begin{array}{l}O{B^2} + S{O^2} = S{B^2}\\{6^2} + S{O^2} = {10^2}\\S{O^2} = 100 - 36 = 64\\SO = 8cm.\end{array}\)
Thể tích của hình nón là \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.6^2}.8 = 96\pi \left( {c{m^3}} \right)\).
Hình nón là một hình học không gian được tạo thành bởi một đỉnh và một đường tròn đáy. Đường thẳng nối đỉnh với tâm đường tròn đáy được gọi là trục của hình nón. Khoảng cách từ đỉnh đến bất kỳ điểm nào trên đường tròn đáy được gọi là đường sinh của hình nón.
Hình nón là hình được tạo bởi mặt nón và một đường tròn. Mặt nón là tập hợp các đường thẳng đi qua một điểm cố định (đỉnh) và tiếp xúc với một đường tròn cố định (đáy).
Diện tích xung quanh của hình nón được tính bằng công thức:
Sxq = πrl
Trong đó:
Diện tích toàn phần của hình nón được tính bằng công thức:
Stp = Sxq + Sđáy = πrl + πr²
Trong đó:
Thể tích của hình nón được tính bằng công thức:
V = (1/3)πr²h
Trong đó:
Bài 1: Một hình nón có bán kính đáy r = 5cm và chiều cao h = 12cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình nón đó.
Giải:
Khi giải các bài toán liên quan đến hình nón, cần chú ý đến việc xác định đúng các yếu tố của hình nón (bán kính đáy, chiều cao, độ dài đường sinh) và sử dụng đúng công thức tính diện tích và thể tích.
Hình nón xuất hiện trong nhiều ứng dụng thực tế như:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết Hình nón Toán 9 Cánh diều. Chúc bạn học tập tốt!