Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 87 SGK Toán 9 tập 2 - Cánh diều tại giaitoan.edu.vn. Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập này thuộc chương trình Toán 9 tập 2, tập trung vào việc rèn luyện kỹ năng giải toán thực tế và áp dụng các kiến thức đã học vào các bài toán cụ thể.
Cắt một miếng bìa có dạng hình lục giác đều A1A2A3A4 A5A6 với tâm O và ghim miếng bìa đó lên bảng tại điểm O (Hình 27). a) Quay miếng bìa đó theo phép quay thuận chiều (60^circ ) tâm O (Hình 28a). Hãy cho biết qua phép quay trên: - Các điểm A1, A2, A3, A4, A5, A6 lần lượt quay đến vị trí mới là các điểm nào. - Hình lục giác đều A1A2A3A4 A5A6 sau khi quay đến một hình mới có trùng với chính nó hay không? b) Quay miếng bìa đó theo phép quay ngược chiều (60^circ ) tâm O (Hình 28b). Hãy ch
Đề bài
Trả lời câu hỏi Hoạt động 2 trang 75 SGK Toán 9 Cánh diều
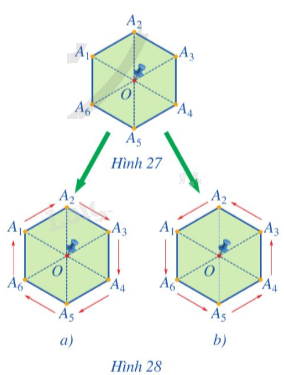
Cắt một miếng bìa có dạng hình lục giác đều A1A2A3A4 A5A6 với tâm O và ghim miếng bìa đó lên bảng tại điểm O (Hình 27).
a) Quay miếng bìa đó theo phép quay thuận chiều \(60^\circ \) tâm O (Hình 28a). Hãy cho biết qua phép quay trên:
- Các điểm A1, A2, A3, A4, A5, A6 lần lượt quay đến vị trí mới là các điểm nào.
- Hình lục giác đều A1A2A3A4A5A6 sau khi quay đến một hình mới có trùng với chính nó hay không?
b) Quay miếng bìa đó theo phép quay ngược chiều \(60^\circ \) tâm O (Hình 28b). Hãy cho biết qua phép quay trên:
- Các điểm A1, A2, A3, A4, A5, A6 lần lượt quay đến vị trí mới là các điểm nào.
- Hình lục giác đều A1A2A3A4A5A6 sau khi quay đến một hình mới có trùng với chính nó hay không?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Xác định điểm đối xứng của mỗi điểm A1, A2, A3, A4, A5, A6 khi quay thuận chiều, ngược chiều qua tâm O.
- Xét xem hình dạng của lục giác đều ban đầu có bị thay đổi so với hình mới tạo thành hay không?
Lời giải chi tiết
a) Phép quay thuận chiều \(60^\circ \) tâm O sẽ biến mỗi điểm A1, A2, A3, A4, A5, A6 thành điểm A2, A3, A4, A5, A6, A1 qua tâm O.
Hình lục giác đều A1A2A3A4A5A6 sau khi quay đến một hình mới trùng với chính nó vì thứ tự các đỉnh thay đổi nhưng hình dạng vẫn giữ nguyên.
b) Phép quay ngược chiều \(60^\circ \) tâm O sẽ biến mỗi điểm A1, A2, A3, A4, A5, A6 thành điểm A6, A1, A2, A3, A4, A5 qua tâm O.
Hình lục giác đều A1A2A3A4A5A6 sau khi quay đến một hình mới trùng với chính nó vì thứ tự các đỉnh thay đổi nhưng hình dạng vẫn giữ nguyên.
Mục 2 trang 87 SGK Toán 9 tập 2 - Cánh diều thường xoay quanh các bài toán liên quan đến hàm số bậc hai, bao gồm việc xác định hệ số, tìm đỉnh parabol, vẽ đồ thị hàm số và giải các bài toán ứng dụng thực tế. Để giải quyết hiệu quả các bài toán này, học sinh cần nắm vững các kiến thức cơ bản về hàm số bậc hai, đặc biệt là công thức tính đỉnh parabol, trục đối xứng và giao điểm với các trục tọa độ.
Bài tập 1: Cho hàm số y = 2x2 - 4x + 1. Tìm tọa độ đỉnh của parabol.
Lời giải:
Bài tập 2: Tìm giao điểm của đồ thị hàm số y = x2 - 3x + 2 với trục Ox.
Lời giải:
Để tìm giao điểm với trục Ox, ta giải phương trình x2 - 3x + 2 = 0.
Δ = (-3)2 - 4(1)(2) = 1
x1 = (3 + √1)/2 = 2
x2 = (3 - √1)/2 = 1
Vậy, giao điểm của đồ thị hàm số với trục Ox là A(1, 0) và B(2, 0).
Để củng cố kiến thức và kỹ năng giải bài tập, các em có thể tự luyện tập thêm với các bài tập tương tự trong SGK Toán 9 tập 2 - Cánh diều và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin hơn khi làm bài kiểm tra.
| Công thức | Mô tả |
|---|---|
| y = ax2 + bx + c | Dạng tổng quát của hàm số bậc hai |
| xI = -b/2a | Hoành độ đỉnh của parabol |
| yI = -Δ/4a | Tung độ đỉnh của parabol |
| Δ = b2 - 4ac | Biệt thức của phương trình bậc hai |
Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trên đây, các em học sinh sẽ hiểu rõ hơn về mục 2 trang 87 SGK Toán 9 tập 2 - Cánh diều và đạt kết quả tốt trong học tập.