Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 1 của giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3 trang 115 và 116 sách giáo khoa Toán 9 tập 1 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Trong Hình 55, đỉnh của góc (AIB) có thuộc đường tròn hay không? Hai cạnh của góc chứa hai dây cung nào của đường tròn?
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 115 SGK Toán 9 Cánh diều
Hãy vẽ một đường tròn và hai góc nội tiếp trong đường tròn đó.
Phương pháp giải:
Dựa vào kiến thức vừa học để vẽ hình.
Lời giải chi tiết:
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 115 SGK Toán 9 Cánh diều
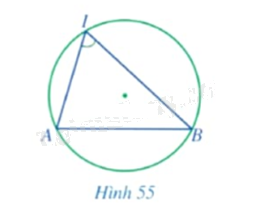
Trong Hình 55, đỉnh của góc \(AIB\) có thuộc đường tròn hay không? Hai cạnh của góc chứa hai dây cung nào của đường tròn?
Phương pháp giải:
Dựa vào hình ảnh trực quan để đưa ra nhận xét.
Lời giải chi tiết:
- Đỉnh của góc \(AIB\) có thuộc đường tròn.
- Hai cạnh của góc chứa hai dây cung \(IA,IB\) của đường tròn.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 4 trang 116SGK Toán 9 Cánh diều
Cho đường tròn \(\left( {O;R} \right)\) và dây cung \(AB = R\). Điểm \(C\) thuộc cung lớn \(AB,C\) khác \(A\) và \(B\). Tính số đo góc \(ACB\).
Phương pháp giải:
Dựa vào kiến thức vừa học về góc nội tiếp và góc ở tâm để tính.
Lời giải chi tiết:
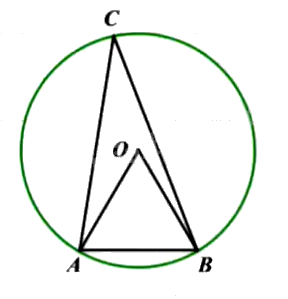
Xét tam giác \(OAB\) có: \(OA = OB = AB = R\).
Suy ra tam giác \(OAB\) là tam giác đều nên \(\widehat {AOB} = 60^\circ \).
Xét đường tròn \(\left( O \right)\): Vì \(\widehat {AOB}\) là góc ở tâm và \(\widehat {ACB}\) là góc nội tiếp cùng chắn cung \(AB\) nên:
\(\widehat {ACB} = \frac{1}{2}\widehat {AOB} = \frac{1}{2}.60^\circ = 30^\circ \).
Vậy \(\widehat {ACB} = 30^\circ \).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 115SGK Toán 9 Cánh diều
Cho góc \(AIB\) nội tiếp đường tròn tâm \(O\) đường kính \(IK\) sao cho tâm \(O\) nằm trong góc đó (Hình 57).
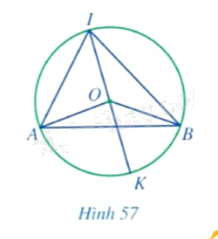
a) Các cặp góc \(\widehat {OAI}\) và \(\widehat {OIA};\widehat {OBI}\) và \(\widehat {OIB}\) có bằng nhau hay không?
b) Tính các tổng \(\widehat {AOI} + 2\widehat {OIA},\widehat {BOI} + 2\widehat {OIB}\).
c) Tính các tổng \(\widehat {AOI} + \widehat {AOK},\widehat {BOI} + \widehat {BOK}\).
d) So sánh \(\widehat {AOK}\) và \(2\widehat {OIA},\widehat {BOK}\) và \(2\widehat {OIB},\widehat {AOB}\) và \(2\widehat {AIB}\).
Phương pháp giải:
Dựa vào các kiến thức đã học về đường tròn để xác định.
Lời giải chi tiết:
a) Do \(OI = OA = R\) nên tam giác \(IOA\) cân tại \(O\) suy ra \(\widehat {OAI} = \widehat {OIA}\)
Do \(OI = OB = R\) nên tam giác \(IOB\) cân tại \(O\) suy ra \(\widehat {OBI} = \widehat {OIB}\)
b) Xét tam giác \(AOI\) cân tại \(O\) có:
\(\widehat {AOI} + \widehat {OIA} + \widehat {OAI} = 180^\circ \Rightarrow \widehat {AOI} + \widehat {OIA} + \widehat {OIA} = 180^\circ \Rightarrow \widehat {AOI} + 2\widehat {OIA} = 180^\circ \)
Xét tam giác \(BOI\) cân tại \(O\) có:
\(\widehat {BOI} + \widehat {OIB} + \widehat {OBI} = 180^\circ \Rightarrow \widehat {BOI} + \widehat {OIB} + \widehat {OIB} = 180^\circ \Rightarrow \widehat {BOI} + 2\widehat {OIB} = 180^\circ \)
c) Ta có: \(\widehat {AOI} + \widehat {AOK} = 180^\circ \) (hai góc kề bù)
\(\widehat {BOI} + \widehat {BOK} = 180^\circ \) (hai góc kề bù)
d) Do \(\widehat {AOI} + 2\widehat {OIA} = 180^\circ \) lại có \(\widehat {AOI} + \widehat {AOK} = 180^\circ \) nên \(2\widehat {OIA} = \widehat {AOK}\)
Do \(\widehat {BOI} + 2\widehat {OIB} = 180^\circ \) lại có \(\widehat {BOI} + \widehat {BOK} = 180^\circ \) nên \(2\widehat {OIB} = \widehat {BOK}\)
Ta có: \(\widehat {OIA} + \widehat {OIB} = \widehat {AIB} \Rightarrow 2\left( {\widehat {OIA} + \widehat {OIB}} \right) = 2\widehat {AIB} \Rightarrow 2\widehat {OIA} + 2\widehat {OIB} = 2\widehat {AIB}\)
Mà \(2\widehat {OIA} = \widehat {AOK},2\widehat {OIB} = \widehat {BOK}\) nên \(\widehat {AOK} + \widehat {BOK} = 2\widehat {AIB} \Rightarrow \widehat {AOB} = 2\widehat {AIB}\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 5 trang 116 SGK Toán 9 Cánh diều
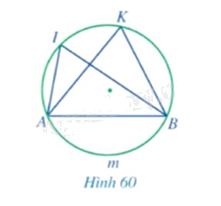
Quan sát Hình 60 và nêu mối liên hệ giữa
a) \(\widehat {AIB}\) và sđ$\overset\frown{AmB}$;
b) \(\widehat {AKB}\) và sđ$\overset\frown{AmB}$;
c) \(\widehat {AIB}\) và \(\widehat {AKB}\).
Phương pháp giải:
Dựa vào kiến thức “Góc nội tiếp có số đo bằng nửa số đo cung bị chắn” để làm bài.
Lời giải chi tiết:
a) Ta thấy: \(\widehat {AIB}\) là góc nội tiếp chắn $\overset\frown{AmB}$ nên $\widehat{AIB}=\frac{1}{2}sđ\overset\frown{AmB}$.
b) Ta thấy: \(\widehat {AKB}\) là góc nội tiếp chắn $\overset\frown{AmB}$ nên $\widehat{AKB}=\frac{1}{2}sđ\overset\frown{AmB}$.
c) Do $\widehat{AIB}=\frac{1}{2}sđ\overset\frown{AmB};\widehat{AKB}=\frac{1}{2}sđ\overset\frown{AmB}$ nên \(\widehat {AIB} = \widehat {AKB}\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 5 trang 119SGK Toán 9 Cánh diều
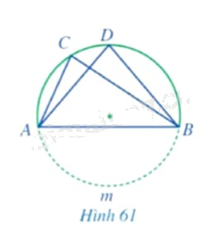
Trong Hình 61, gọi \(I\) là giao điểm của \(AD\) và \(BC\). Chứng minh \(IA.ID = IB.IC\).
Phương pháp giải:
Dựa vào tính chất góc nội tiếp để chứng minh.
Lời giải chi tiết:
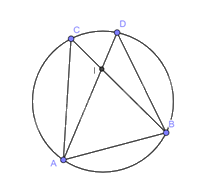
Ta có: \(\widehat {ACB}\) và \(\widehat {ADB}\) là hai góc nội tiếp chắn cung \(AB\) nên \(\widehat {ACB} = \widehat {ADB}\) hay \(\widehat {ACI} = \widehat {BDI}\).
Do \(\widehat {CIA}\) và \(\widehat {DIB}\) là hai góc đối đỉnh nên \(\widehat {CIA} = \widehat {DIB}\).
Xét \(\Delta CIA\) và \(\Delta DIB\) có:
$\left\{ \begin{align}\widehat{ACI}=\widehat{BDI} \\ \widehat{CIA}=\widehat{DIB} \end{align} \right.\Rightarrow \Delta CIA\backsim \Delta DIB\left( g.g \right) \Rightarrow \frac{CI}{DI}=\frac{IA}{IB}\Rightarrow IA.ID=IC.IB.$
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 115 SGK Toán 9 Cánh diều
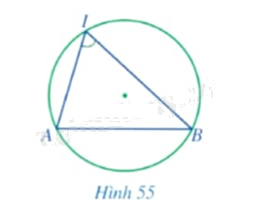
Trong Hình 55, đỉnh của góc \(AIB\) có thuộc đường tròn hay không? Hai cạnh của góc chứa hai dây cung nào của đường tròn?
Phương pháp giải:
Dựa vào hình ảnh trực quan để đưa ra nhận xét.
Lời giải chi tiết:
- Đỉnh của góc \(AIB\) có thuộc đường tròn.
- Hai cạnh của góc chứa hai dây cung \(IA,IB\) của đường tròn.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 115 SGK Toán 9 Cánh diều
Hãy vẽ một đường tròn và hai góc nội tiếp trong đường tròn đó.
Phương pháp giải:
Dựa vào kiến thức vừa học để vẽ hình.
Lời giải chi tiết:
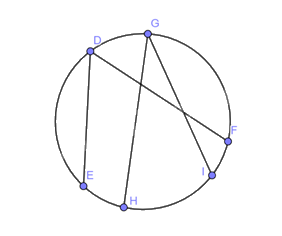
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 115SGK Toán 9 Cánh diều
Cho góc \(AIB\) nội tiếp đường tròn tâm \(O\) đường kính \(IK\) sao cho tâm \(O\) nằm trong góc đó (Hình 57).
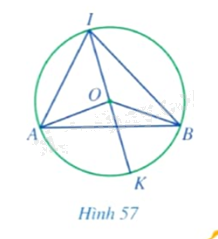
a) Các cặp góc \(\widehat {OAI}\) và \(\widehat {OIA};\widehat {OBI}\) và \(\widehat {OIB}\) có bằng nhau hay không?
b) Tính các tổng \(\widehat {AOI} + 2\widehat {OIA},\widehat {BOI} + 2\widehat {OIB}\).
c) Tính các tổng \(\widehat {AOI} + \widehat {AOK},\widehat {BOI} + \widehat {BOK}\).
d) So sánh \(\widehat {AOK}\) và \(2\widehat {OIA},\widehat {BOK}\) và \(2\widehat {OIB},\widehat {AOB}\) và \(2\widehat {AIB}\).
Phương pháp giải:
Dựa vào các kiến thức đã học về đường tròn để xác định.
Lời giải chi tiết:
a) Do \(OI = OA = R\) nên tam giác \(IOA\) cân tại \(O\) suy ra \(\widehat {OAI} = \widehat {OIA}\)
Do \(OI = OB = R\) nên tam giác \(IOB\) cân tại \(O\) suy ra \(\widehat {OBI} = \widehat {OIB}\)
b) Xét tam giác \(AOI\) cân tại \(O\) có:
\(\widehat {AOI} + \widehat {OIA} + \widehat {OAI} = 180^\circ \Rightarrow \widehat {AOI} + \widehat {OIA} + \widehat {OIA} = 180^\circ \Rightarrow \widehat {AOI} + 2\widehat {OIA} = 180^\circ \)
Xét tam giác \(BOI\) cân tại \(O\) có:
\(\widehat {BOI} + \widehat {OIB} + \widehat {OBI} = 180^\circ \Rightarrow \widehat {BOI} + \widehat {OIB} + \widehat {OIB} = 180^\circ \Rightarrow \widehat {BOI} + 2\widehat {OIB} = 180^\circ \)
c) Ta có: \(\widehat {AOI} + \widehat {AOK} = 180^\circ \) (hai góc kề bù)
\(\widehat {BOI} + \widehat {BOK} = 180^\circ \) (hai góc kề bù)
d) Do \(\widehat {AOI} + 2\widehat {OIA} = 180^\circ \) lại có \(\widehat {AOI} + \widehat {AOK} = 180^\circ \) nên \(2\widehat {OIA} = \widehat {AOK}\)
Do \(\widehat {BOI} + 2\widehat {OIB} = 180^\circ \) lại có \(\widehat {BOI} + \widehat {BOK} = 180^\circ \) nên \(2\widehat {OIB} = \widehat {BOK}\)
Ta có: \(\widehat {OIA} + \widehat {OIB} = \widehat {AIB} \Rightarrow 2\left( {\widehat {OIA} + \widehat {OIB}} \right) = 2\widehat {AIB} \Rightarrow 2\widehat {OIA} + 2\widehat {OIB} = 2\widehat {AIB}\)
Mà \(2\widehat {OIA} = \widehat {AOK},2\widehat {OIB} = \widehat {BOK}\) nên \(\widehat {AOK} + \widehat {BOK} = 2\widehat {AIB} \Rightarrow \widehat {AOB} = 2\widehat {AIB}\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 4 trang 116SGK Toán 9 Cánh diều
Cho đường tròn \(\left( {O;R} \right)\) và dây cung \(AB = R\). Điểm \(C\) thuộc cung lớn \(AB,C\) khác \(A\) và \(B\). Tính số đo góc \(ACB\).
Phương pháp giải:
Dựa vào kiến thức vừa học về góc nội tiếp và góc ở tâm để tính.
Lời giải chi tiết:
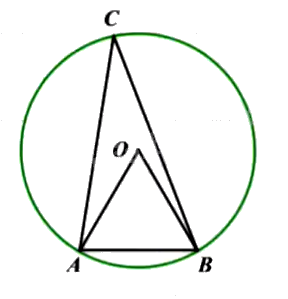
Xét tam giác \(OAB\) có: \(OA = OB = AB = R\).
Suy ra tam giác \(OAB\) là tam giác đều nên \(\widehat {AOB} = 60^\circ \).
Xét đường tròn \(\left( O \right)\): Vì \(\widehat {AOB}\) là góc ở tâm và \(\widehat {ACB}\) là góc nội tiếp cùng chắn cung \(AB\) nên:
\(\widehat {ACB} = \frac{1}{2}\widehat {AOB} = \frac{1}{2}.60^\circ = 30^\circ \).
Vậy \(\widehat {ACB} = 30^\circ \).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 5 trang 116 SGK Toán 9 Cánh diều
Quan sát Hình 60 và nêu mối liên hệ giữa
a) \(\widehat {AIB}\) và sđ$\overset\frown{AmB}$;
b) \(\widehat {AKB}\) và sđ$\overset\frown{AmB}$;
c) \(\widehat {AIB}\) và \(\widehat {AKB}\).
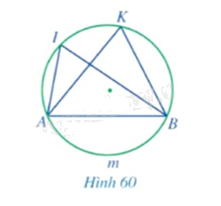
Phương pháp giải:
Dựa vào kiến thức “Góc nội tiếp có số đo bằng nửa số đo cung bị chắn” để làm bài.
Lời giải chi tiết:
a) Ta thấy: \(\widehat {AIB}\) là góc nội tiếp chắn $\overset\frown{AmB}$ nên $\widehat{AIB}=\frac{1}{2}sđ\overset\frown{AmB}$.
b) Ta thấy: \(\widehat {AKB}\) là góc nội tiếp chắn $\overset\frown{AmB}$ nên $\widehat{AKB}=\frac{1}{2}sđ\overset\frown{AmB}$.
c) Do $\widehat{AIB}=\frac{1}{2}sđ\overset\frown{AmB};\widehat{AKB}=\frac{1}{2}sđ\overset\frown{AmB}$ nên \(\widehat {AIB} = \widehat {AKB}\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 5 trang 119SGK Toán 9 Cánh diều
Trong Hình 61, gọi \(I\) là giao điểm của \(AD\) và \(BC\). Chứng minh \(IA.ID = IB.IC\).
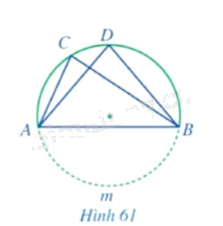
Phương pháp giải:
Dựa vào tính chất góc nội tiếp để chứng minh.
Lời giải chi tiết:
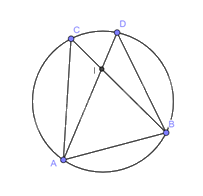
Ta có: \(\widehat {ACB}\) và \(\widehat {ADB}\) là hai góc nội tiếp chắn cung \(AB\) nên \(\widehat {ACB} = \widehat {ADB}\) hay \(\widehat {ACI} = \widehat {BDI}\).
Do \(\widehat {CIA}\) và \(\widehat {DIB}\) là hai góc đối đỉnh nên \(\widehat {CIA} = \widehat {DIB}\).
Xét \(\Delta CIA\) và \(\Delta DIB\) có:
$\left\{ \begin{align}\widehat{ACI}=\widehat{BDI} \\ \widehat{CIA}=\widehat{DIB} \end{align} \right.\Rightarrow \Delta CIA\backsim \Delta DIB\left( g.g \right) \Rightarrow \frac{CI}{DI}=\frac{IA}{IB}\Rightarrow IA.ID=IC.IB.$
Mục 3 trong SGK Toán 9 tập 1 - Cánh diều thường tập trung vào một chủ đề cụ thể, ví dụ như hệ phương trình bậc hai hai ẩn, hoặc các bài toán liên quan đến hàm số bậc nhất. Việc nắm vững lý thuyết và phương pháp giải là yếu tố then chốt để giải quyết các bài tập trong mục này.
Trước khi đi vào giải bài tập, chúng ta cần ôn lại những kiến thức lý thuyết quan trọng. Ví dụ, nếu mục 3 liên quan đến hệ phương trình bậc hai hai ẩn, chúng ta cần nhớ lại các phương pháp giải như phương pháp thế, phương pháp cộng đại số, và điều kiện để hệ phương trình có nghiệm duy nhất, vô nghiệm hoặc vô số nghiệm.
Mỗi bài tập trong mục 3 sẽ có những yêu cầu và đặc điểm riêng. Việc phân tích kỹ đề bài, xác định đúng dữ kiện và yêu cầu là bước đầu tiên quan trọng. Sau đó, chúng ta cần lựa chọn phương pháp giải phù hợp nhất. Ví dụ, nếu bài toán yêu cầu tìm nghiệm của hệ phương trình, chúng ta có thể sử dụng phương pháp thế hoặc phương pháp cộng đại số. Nếu bài toán yêu cầu chứng minh một đẳng thức, chúng ta cần biến đổi vế này thành vế kia hoặc sử dụng các công thức đại số.
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 3 trang 115 và 116 SGK Toán 9 tập 1 - Cánh diều:
Để củng cố kiến thức và kỹ năng giải toán, các em nên luyện tập thêm các bài tập tương tự. Các em có thể tìm thấy các bài tập này trong sách bài tập Toán 9 tập 1, hoặc trên các trang web học toán online uy tín như giaitoan.edu.vn.
Khi giải bài tập Toán 9, các em cần chú ý những điều sau:
Các kiến thức và kỹ năng giải toán trong mục 3 có ứng dụng rất lớn trong thực tế. Ví dụ, hệ phương trình bậc hai hai ẩn được sử dụng để giải các bài toán về kinh tế, kỹ thuật, và khoa học. Việc nắm vững kiến thức này sẽ giúp các em giải quyết các vấn đề thực tế một cách hiệu quả.
Trong mục 3, các em có thể gặp các dạng bài tập sau:
Để tự học hiệu quả, các em nên:
Hy vọng rằng với lời giải chi tiết và những hướng dẫn trên, các em sẽ hiểu rõ hơn về mục 3 trang 115, 116 SGK Toán 9 tập 1 - Cánh diều và có thể tự tin giải các bài tập tương tự. Chúc các em học tập tốt!