Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn giải bài tập 7 trang 81 SGK Toán 9 tập 1 - Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để bạn có thể hiểu rõ bản chất của bài toán.
Cho góc nhọn (alpha ). Biết rằng, tam giác (ABC) vuông tại (A) sao cho (widehat B = alpha ). a) Biểu diễn các tỉ số lượng giác của góc nhọn (alpha ) theo (AB,BC,CA). b) Chứng minh: ({sin ^2}alpha + {cos ^2}alpha = 1;tan alpha = frac{{sin alpha }}{{cos alpha }};cot alpha = frac{{cos alpha }}{{sin alpha }};tan alpha .cot alpha = 1). Từ đó, tính giá trị biểu thức: (S = {sin ^2}35^circ + {cos ^2}35^circ ;T = tan 61^circ .cot 61^circ ).
Đề bài
Cho góc nhọn \(\alpha \). Biết rằng, tam giác \(ABC\) vuông tại \(A\) sao cho \(\widehat B = \alpha \).
a) Biểu diễn các tỉ số lượng giác của góc nhọn \(\alpha \) theo \(AB,BC,CA\).
b) Chứng minh: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\); \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\); \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}\); \(\tan \alpha .\cot \alpha = 1\).
Từ đó, tính giá trị biểu thức: \(S = {\sin ^2}35^\circ + {\cos ^2}35^\circ \); \(T = \tan 61^\circ .\cot 61^\circ \).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào định nghĩa tỉ số lượng giác để làm bài toán.
Lời giải chi tiết
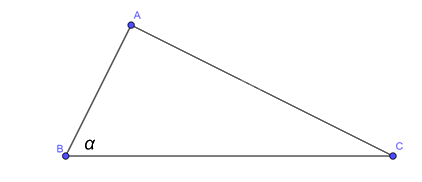
a) \(\sin \alpha = \frac{{AC}}{{BC}}\); \(\cos \alpha = \frac{{AB}}{{BC}}\); \(\tan \alpha = \frac{{AC}}{{AB}}\); \(\cot \alpha = \frac{{AB}}{{AC}}\).
b) Ta có:
\({\sin ^2}\alpha + {\cos ^2}\alpha = {\left( {\frac{{AC}}{{BC}}} \right)^2} + {\left( {\frac{{AB}}{{BC}}} \right)^2} = \frac{{A{C^2} + A{B^2}}}{{B{C^2}}} = \frac{{B{C^2}}}{{B{C^2}}} = 1\).
\(\frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{AC}}{{BC}}:\frac{{AB}}{{BC}} = \frac{{AC}}{{BC}}.\frac{{BC}}{{AB}} = \frac{{AC}}{{AB}} = \tan \alpha \).
\(\frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{AB}}{{BC}}:\frac{{AC}}{{BC}} = \frac{{AB}}{{BC}}.\frac{{BC}}{{AC}} = \frac{{AB}}{{AC}} = \cot \alpha \).
\(\tan \alpha .\cot \alpha = \frac{{AC}}{{AB}}.\frac{{AB}}{{AC}} = 1\).
\(S = {\sin ^2}35^\circ + {\cos ^2}35^\circ = 1\).
\(T = \tan 61^\circ .\cot 61^\circ = 1\).
Bài tập 7 trang 81 SGK Toán 9 tập 1 - Cánh diều thuộc chương trình đại số, tập trung vào việc giải phương trình bậc hai một ẩn. Để giải quyết bài tập này, học sinh cần nắm vững các kiến thức về phương trình bậc hai, công thức nghiệm và các phương pháp giải phương trình.
Bài tập 7 thường bao gồm các phương trình bậc hai với các hệ số khác nhau. Yêu cầu của bài tập là tìm nghiệm của phương trình hoặc xác định điều kiện để phương trình có nghiệm.
Có nhiều phương pháp để giải phương trình bậc hai, bao gồm:
x1,2 = (-b ± √(b2 - 4ac)) / 2a
Ví dụ: Giải phương trình 2x2 - 5x + 2 = 0
Giải:
Để củng cố kiến thức về phương trình bậc hai, bạn có thể luyện tập thêm các bài tập sau:
Bài tập 7 trang 81 SGK Toán 9 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải phương trình bậc hai. Hy vọng với hướng dẫn chi tiết này, bạn đã có thể giải quyết bài tập một cách dễ dàng và hiệu quả. Chúc bạn học tốt!
| Phương pháp | Ưu điểm | Nhược điểm |
|---|---|---|
| Phân tích thành nhân tử | Nhanh chóng, dễ hiểu | Không phải lúc nào cũng áp dụng được |
| Công thức nghiệm | Tổng quát, áp dụng được cho mọi phương trình | Cần tính toán cẩn thận |
| Hoàn thiện bình phương | Giúp hiểu rõ bản chất của phương trình | Phức tạp hơn các phương pháp khác |