Chào mừng bạn đến với bài học lý thuyết Hàm số y = ax² (a ≠ 0) trong chương trình Toán 9 Cánh diều. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về hàm số bậc hai, giúp bạn hiểu rõ hơn về tính chất, đồ thị và ứng dụng của hàm số này.
Chúng ta sẽ cùng nhau khám phá định nghĩa, các yếu tố của hàm số, cách vẽ đồ thị và các bài tập minh họa để củng cố kiến thức đã học.
1. Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) xác định với mọi giá trị x thuộc \(\mathbb{R}\).
1. Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)xác định với mọi giá trị x thuộc \(\mathbb{R}\). |
Ví dụ: Hàm số \(y = 2{x^2},y = - \frac{3}{2}{x^2}\) là các hàm số có dạng \(y = a{x^2}\left( {a \ne 0} \right)\).
2. Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
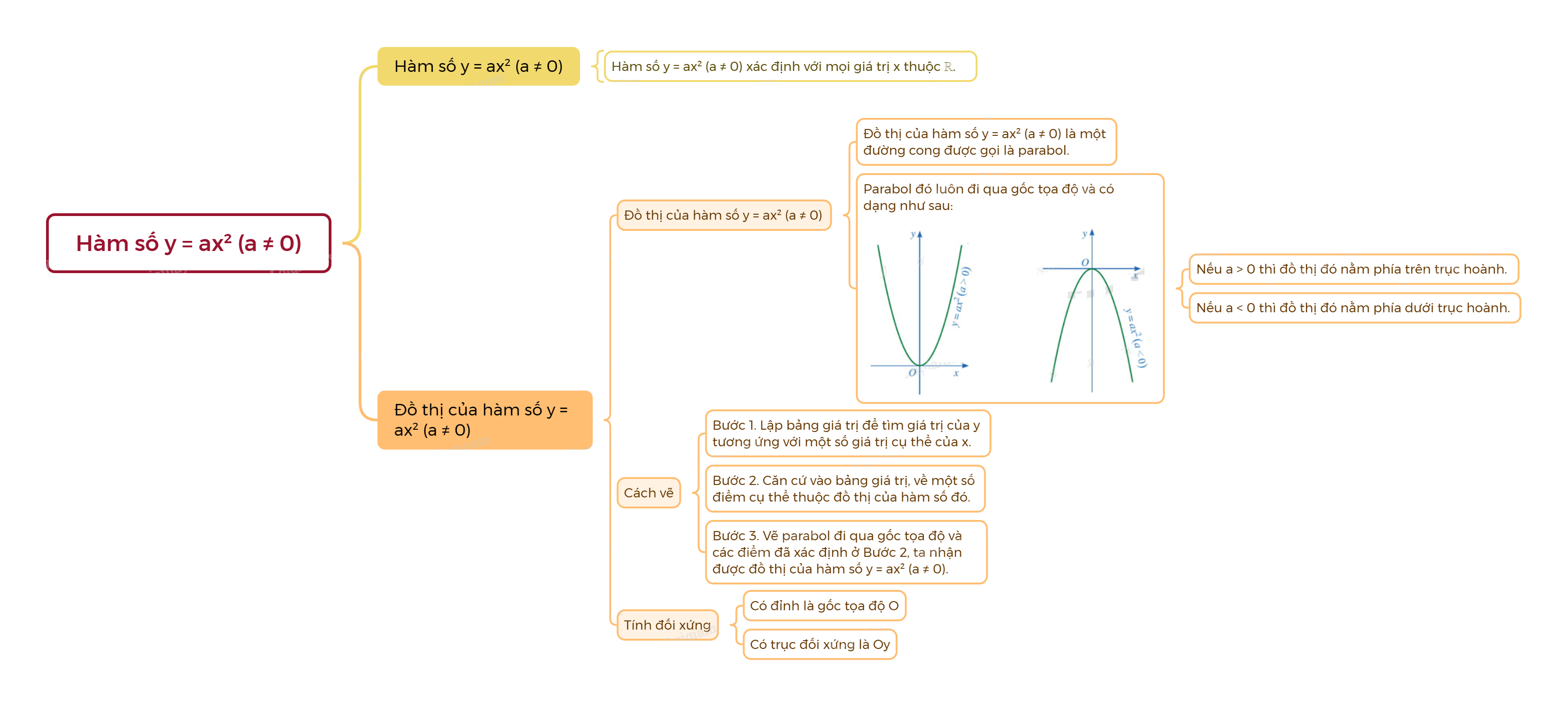
- Đồ thị của hàm số \(y = a{x^2}\) \(\left( {a \ne 0} \right)\) là một đường cong được gọi là parabol. Parabol đó luôn đi qua gốc tọa độ và có dạng như sau:
- Nếu a > 0 thì đồ thị đó nằm phía trên trục hoành. - Nếu a < 0 thì đồ thị đó nằm phía dưới trục hoành. |
Cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
Bước 1. Lập bảng giá trị để tìm giá trị của y tương ứng với một số giá trị cụ thể của x. Bước 2. Căn cứ vào bảng giá trị, về một số điểm cụ thể thuộc đồ thị của hàm số đó. Bước 3. Vẽ parabol đi qua gốc tọa độ và các điểm đã xác định ở Bước 2, ta nhận được đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\). |
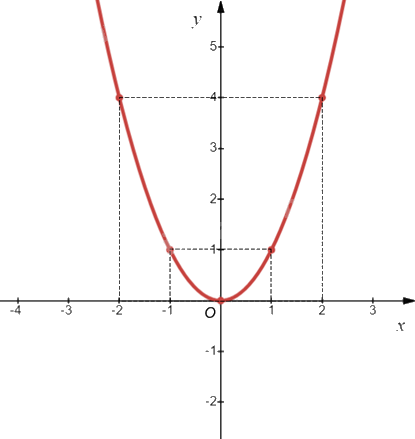
Ví dụ: Vẽ đồ thị của hàm số \(y = {x^2}\).
Bảng giá trị của hàm số:

Biểu diễn các điểm \(\left( { - 2;4} \right)\), \(\left( { - 1;1} \right)\), \(\left( {0;0} \right)\), \(\left( {1;1} \right)\), \(\left( {2;4} \right)\) trên mặt phẳng tọa độ Oxy và nối chúng lại với nhau, ta được đồ thị hàm số \(y = {x^2}\) như hình vẽ sau:
Tính chất
Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) là một parabol đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng. |
Hàm số y = ax² (a ≠ 0) là một trong những hàm số quan trọng nhất trong chương trình Toán 9. Hiểu rõ lý thuyết về hàm số này là nền tảng để giải quyết các bài toán liên quan đến hàm số bậc hai, đồ thị hàm số và ứng dụng thực tế.
Hàm số bậc hai có dạng y = ax² + bx + c, trong đó a, b, c là các số thực và a ≠ 0. Trong trường hợp đặc biệt y = ax² (a ≠ 0), hàm số được gọi là hàm số bậc hai đơn giản. Hàm số này được xác định với mọi giá trị của x.
Tính chất của hàm số phụ thuộc vào giá trị của a:
Đồ thị của hàm số y = ax² (a ≠ 0) là một parabol có đỉnh tại gốc tọa độ O(0; 0) và trục đối xứng là trục Oy. Để vẽ đồ thị, ta có thể thực hiện các bước sau:
Ví dụ 1: Vẽ đồ thị hàm số y = 2x². Vì a = 2 > 0, parabol hướng lên trên. Bảng giá trị:
| x | y |
|---|---|
| -2 | 8 |
| -1 | 2 |
| 0 | 0 |
| 1 | 2 |
| 2 | 8 |
Ví dụ 2: Vẽ đồ thị hàm số y = -x². Vì a = -1 < 0, parabol hướng xuống dưới. Bảng giá trị tương tự như ví dụ 1.
Hàm số y = ax² (a ≠ 0) có nhiều ứng dụng trong thực tế, ví dụ như:
Hãy tự giải các bài tập sau để củng cố kiến thức về hàm số y = ax² (a ≠ 0):
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về lý thuyết Hàm số y = ax² (a ≠ 0) Toán 9 Cánh diều. Chúc bạn học tốt!