Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 95, 96 SGK Toán 9 tập 1 - Cánh diều trên giaitoan.edu.vn. Chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Bài tập này thuộc chương trình học Toán 9 tập 1, tập trung vào việc rèn luyện kỹ năng giải toán và áp dụng kiến thức đã học vào thực tế.
Cho đường tròn (left( {O;R} right)) a) Vẽ đường thẳng (d) đi qua tâm (O) cắt đường tròn tại (A,B). So sánh (OA) và (OB) (Hình 7). b) Giả sử (M) là một điểm tùy ý trên đường tròn (left( {O;R} right)). Trên tia đối của tia (OM), ta lấy điểm (N) sao cho (ON = OM). Điểm (N) có thuộc đường tròn (left( {O;R} right)) hay không?
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 96 SGK Toán 9 Cánh diều
Bạn Hoa có một tờ giấy hình tròn. Nêu cách gấp giấy để xác định tâm đường tròn đó.
Phương pháp giải:
Dựa vào đường tròn là hình có trục đối xứng để gấp.
Lời giải chi tiết:
Ta gấp tờ giấy làm đôi sau đó gấp đôi thêm một lần nữa. Giao điểm của hai lần gấp chính là tâm của đường tròn.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 95SGK Toán 9 Cánh diều
Cho đường tròn \(\left( {O;R} \right)\)
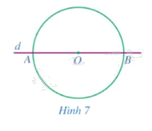
a) Vẽ đường thẳng \(d\) đi qua tâm \(O\) cắt đường tròn tại \(A,B\). So sánh \(OA\) và \(OB\) (Hình 7).
b) Giả sử \(M\) là một điểm tùy ý trên đường tròn \(\left( {O;R} \right)\). Trên tia đối của tia \(OM\), ta lấy điểm \(N\) sao cho \(ON = OM\). Điểm \(N\) có thuộc đường tròn \(\left( {O;R} \right)\) hay không?
Phương pháp giải:
Dựa vào hình ảnh trực quan để trả lời bài toán.
Lời giải chi tiết:
a) \(OA = OB = R\).
b) Do \(OM = R\) lại có \(ON = OM\) nên \(ON = R\). Vậy \(N\) thuộc đường tròn \(\left( {O;R} \right)\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 95 SGK Toán 9 Cánh diều
Cho đường tròn \(\left( {O;R} \right)\). Giả sử \(d\) là đường thẳng đi qua tâm \(O\) và \(M\) là một điểm tùy ý trên đường tròn \(\left( {O;R} \right)\). Kẻ \(MH \bot d\left( {H \in d} \right)\). Trên tia \(MH\) lấy điểm \(N\) sao cho \(H\) là trung điểm của \(MN\) (ta gọi điểm \(N\) là điểm đối xứng với điểm \(M\) qua đường thẳng \(d\)). Điểm \(N\) có thuộc đường tròn \(\left( {O;R} \right)\) hay không?
Phương pháp giải:
Dựa vào kiến thức vừa học để trả lời câu hỏi.
Lời giải chi tiết:
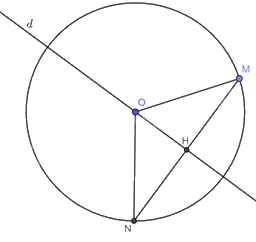
Do \(OH \bot MN\), \(MH = HN\) nên \(OH\) là đường trung trực của \(MN\). Vậy \(OM = ON\).
Lại có \(OM = R\) nên \(ON = R\). Vậy \(N\) có thuộc đường tròn \(\left( {O;R} \right)\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 95SGK Toán 9 Cánh diều
Cho đường tròn \(\left( {O;R} \right)\)
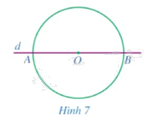
a) Vẽ đường thẳng \(d\) đi qua tâm \(O\) cắt đường tròn tại \(A,B\). So sánh \(OA\) và \(OB\) (Hình 7).
b) Giả sử \(M\) là một điểm tùy ý trên đường tròn \(\left( {O;R} \right)\). Trên tia đối của tia \(OM\), ta lấy điểm \(N\) sao cho \(ON = OM\). Điểm \(N\) có thuộc đường tròn \(\left( {O;R} \right)\) hay không?
Phương pháp giải:
Dựa vào hình ảnh trực quan để trả lời bài toán.
Lời giải chi tiết:
a) \(OA = OB = R\).
b) Do \(OM = R\) lại có \(ON = OM\) nên \(ON = R\). Vậy \(N\) thuộc đường tròn \(\left( {O;R} \right)\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 95 SGK Toán 9 Cánh diều
Cho đường tròn \(\left( {O;R} \right)\). Giả sử \(d\) là đường thẳng đi qua tâm \(O\) và \(M\) là một điểm tùy ý trên đường tròn \(\left( {O;R} \right)\). Kẻ \(MH \bot d\left( {H \in d} \right)\). Trên tia \(MH\) lấy điểm \(N\) sao cho \(H\) là trung điểm của \(MN\) (ta gọi điểm \(N\) là điểm đối xứng với điểm \(M\) qua đường thẳng \(d\)). Điểm \(N\) có thuộc đường tròn \(\left( {O;R} \right)\) hay không?
Phương pháp giải:
Dựa vào kiến thức vừa học để trả lời câu hỏi.
Lời giải chi tiết:
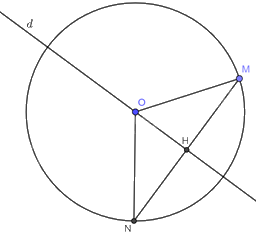
Do \(OH \bot MN\), \(MH = HN\) nên \(OH\) là đường trung trực của \(MN\). Vậy \(OM = ON\).
Lại có \(OM = R\) nên \(ON = R\). Vậy \(N\) có thuộc đường tròn \(\left( {O;R} \right)\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 96 SGK Toán 9 Cánh diều
Bạn Hoa có một tờ giấy hình tròn. Nêu cách gấp giấy để xác định tâm đường tròn đó.
Phương pháp giải:
Dựa vào đường tròn là hình có trục đối xứng để gấp.
Lời giải chi tiết:
Ta gấp tờ giấy làm đôi sau đó gấp đôi thêm một lần nữa. Giao điểm của hai lần gấp chính là tâm của đường tròn.
Mục 3 trang 95, 96 SGK Toán 9 tập 1 - Cánh diều tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 1 yêu cầu học sinh xác định hệ số của hàm số bậc nhất. Để giải bài này, học sinh cần nắm vững dạng tổng quát của hàm số bậc nhất: y = ax + b, trong đó a và b là các hệ số. Học sinh cần xác định đúng giá trị của a và b để đưa ra kết quả chính xác.
Bài 2 yêu cầu học sinh vẽ đồ thị của hàm số bậc nhất. Để vẽ đồ thị, học sinh cần xác định ít nhất hai điểm thuộc đồ thị. Có thể chọn hai điểm bất kỳ, hoặc sử dụng các điểm đặc biệt như giao điểm với trục hoành và trục tung.
Bài 3 là một bài toán ứng dụng, yêu cầu học sinh sử dụng hàm số bậc nhất để giải quyết một bài toán thực tế. Học sinh cần phân tích đề bài, xác định các yếu tố liên quan đến hàm số, và xây dựng phương trình hàm số phù hợp.
Bài 4 yêu cầu học sinh so sánh các hàm số bậc nhất. Để so sánh, học sinh có thể dựa vào hệ số a của hàm số. Nếu a > 0, hàm số đồng biến; nếu a < 0, hàm số nghịch biến.
Khi giải bài tập về hàm số bậc nhất, học sinh cần lưu ý một số điểm sau:
Ngoài SGK Toán 9 tập 1 - Cánh diều, học sinh có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức về hàm số bậc nhất:
Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trên đây, các em học sinh sẽ tự tin hơn khi giải các bài tập về hàm số bậc nhất trong SGK Toán 9 tập 1 - Cánh diều. Chúc các em học tập tốt!