Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 2 trang 89 sách giáo khoa Toán 9 tập 2 của nhà xuất bản Cánh diều.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải một cách cẩn thận, kèm theo các bước giải chi tiết và giải thích rõ ràng để giúp bạn nắm vững kiến thức.
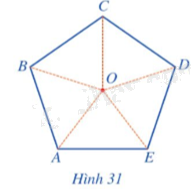
Cho ngũ giác ABCDE tâm O (Hình 31). a) Phép quay ngược chiều tâm O biến điểm A thành điểm E thì các điểm B, C, D, E tương ứng biến thành các điểm nào? b) Chỉ ra các phép quay tâm O giữ nguyên hình ngũ giác đều đã cho.
Đề bài
Cho ngũ giác ABCDE tâm O (Hình 31).
a) Phép quay ngược chiều tâm O biến điểm A thành điểm E thì các điểm B, C, D, E tương ứng biến thành các điểm nào?
b) Chỉ ra các phép quay tâm O giữ nguyên hình ngũ giác đều đã cho.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Xác định \(a^\circ \) trong “Phép quay ngược chiều \(a^\circ \) tâm O biến điểm A thành điểm E”.
Các trường hợp còn lại tương tự.
b) Các phép quay thuận chiều \(a^\circ \) tâm O và các phép quay ngược chiều \(a^\circ \) tâm O, với \(a^\circ \) nhận các giá trị:
\({a_1}^\circ = \frac{{360^\circ }}{5},{a_2}^\circ = \frac{{2.360^\circ }}{5},{a_3}^\circ = \frac{{3.360^\circ }}{5},{a_4}^\circ = \frac{{4.360^\circ }}{5},{a_5}^\circ = \frac{{5.360^\circ }}{5}.\)
Lời giải chi tiết
a) Vì ABCDE là ngũ giác đều nên:
OA = OB = OC = OD = OE
AB = BC = CD = DE = EA
Suy ra \( \widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat { DOE} = \widehat {EOA} = \frac{360^\circ}{5} = 72^\circ\)
Khi đó, phép quay ngược chiều \(72^\circ\) biến các điểm B, C, D, E thành các điểm A, B, C, D.
b) Các phép quay tâm O giữ nguyên hình ngũ giác đều:
Phép quay thuận chiều \(72^\circ ,144^\circ ,216^\circ ,288^\circ ,360^\circ \) tâm O.
Phép quay ngược chiều \(72^\circ ,144^\circ ,216^\circ ,288^\circ ,360^\circ \) tâm O.
Bài tập 2 trang 89 SGK Toán 9 tập 2 - Cánh diều thuộc chương trình học về hàm số bậc hai. Bài tập này yêu cầu học sinh vận dụng kiến thức về parabol, đỉnh của parabol, trục đối xứng và các điểm đặc biệt của parabol để giải quyết các bài toán thực tế.
Bài tập 2 bao gồm các câu hỏi liên quan đến việc xác định các yếu tố của parabol dựa trên phương trình của nó. Cụ thể, học sinh cần:
Để giải bài tập 2 trang 89 SGK Toán 9 tập 2 - Cánh diều một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
Bài 2: Xác định a, b, c của mỗi hàm số sau:
Lời giải:
Ví dụ: Cho hàm số y = x2 - 4x + 3. Hãy xác định tọa độ đỉnh của parabol.
Lời giải:
Hệ số a = 1, b = -4, c = 3.
Tọa độ đỉnh của parabol là:
xđỉnh = -b / (2a) = -(-4) / (2 * 1) = 2
yđỉnh = (4ac - b2) / (4a) = (4 * 1 * 3 - (-4)2) / (4 * 1) = (12 - 16) / 4 = -1
Vậy tọa độ đỉnh của parabol là (2; -1).
Bài tập 2 trang 89 SGK Toán 9 tập 2 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai. Hy vọng với lời giải chi tiết và các phương pháp giải đã trình bày, bạn sẽ tự tin giải quyết bài tập này một cách hiệu quả.