Chào mừng bạn đến với bài học lý thuyết về căn bậc hai và căn bậc ba của số thực trong chương trình Toán 9 Cánh diều. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng quan trọng, giúp bạn giải quyết các bài toán liên quan một cách hiệu quả.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất và các ứng dụng thực tế của căn bậc hai và căn bậc ba, đồng thời luyện tập thông qua các ví dụ minh họa chi tiết.
1. Căn bậc hai của số thực không âm Căn bậc hai của số thực a không âm là số thực x sao cho \({x^2} = a\).
1. Căn bậc hai của số thực không âm
Căn bậc hai của số thực a không âm là số thực x sao cho \({x^2} = a\). |
Chú ý:
- Khi \(a > 0\), số a có đúng hai căn bậc hai là hai số đối nhau: số dương kí hiệu là \(\sqrt a \); số âm kí hiệu là \( - \sqrt a \). Ta gọi \(\sqrt a \) là căn bậc hai số học của a.
- Căn bậc hai của số 0 bằng 0.
- Số âm không có căn bậc hai.
Ví dụ:
· \(\sqrt {81} = 9\) nên 81 có hai căn bậc hai là 9 và -9.
· Căn bậc hai số học của 121 là \(\sqrt {121} = 11\).
Nhận xét: Với hai số a, b không âm, ta có:
- Nếu \(a < b\) thì \(\sqrt a < \sqrt b \);
- Nếu \(\sqrt a < \sqrt b \) thì \(a < b\).
2. Căn bậc ba
Khái niệm căn bậc ba của một số thực
Căn bậc ba của số thực a là số thực x sao cho \({x^3} = a\). Căn bậc ba của một số thực a được kí hiệu là \(\sqrt[3]{a}\) |
Chú ý: Mỗi số thực a đều có duy nhất một căn bậc ba.
Nhận xét: \({\left( {\sqrt[3]{a}} \right)^3} = a\).
Với hai số a, b, ta có:
- Nếu \(a < b\) thì \(\sqrt[3]{a} < \sqrt[3]{b}\).
- Nếu \(\sqrt[3]{a} < \sqrt[3]{b}\) thì \(a < b\).
Ví dụ:
\(\sqrt[3]{{64}} = \sqrt[3]{{{4^3}}} = 4\);
\(\sqrt[3]{{ - 27}} = \sqrt[3]{{{{\left( { - 3} \right)}^3}}} = - 3\).
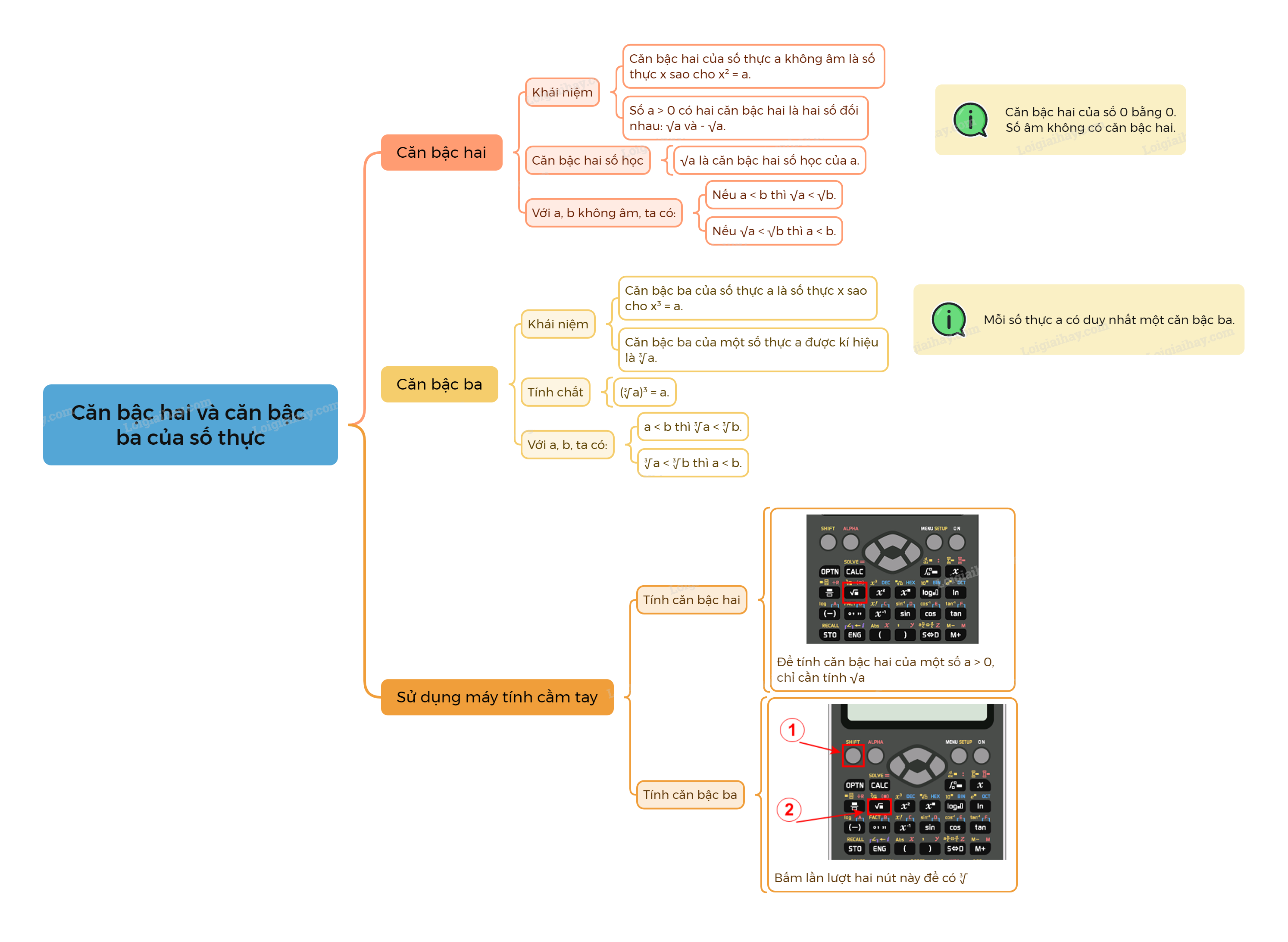
3. Sử dụng máy tính cầm tay để tìm căn bậc hai, căn bậc ba của một số hữu tỉ
Tính căn bậc hai của một số bằng máy tính cầm tay
Để tính các căn bậc hai của một số \(a > 0\), chỉ cần tính \(\sqrt a \). Có thể dễ dàng làm điều này bằng cách sử dụng MTCT.
Sử dụng nút này để bấm căn bậc hai. |
Tính căn bậc ba của một số bằng máy tính cầm tay
Ta có thể sử dụng loại MTCT thích hợp để tính căn bậc ba của một số.

Ví dụ:
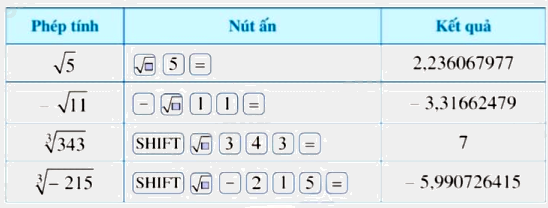
Trong chương trình Toán 9, phần lý thuyết về căn bậc hai và căn bậc ba của số thực đóng vai trò quan trọng, là nền tảng cho việc giải quyết nhiều bài toán phức tạp hơn. Bài viết này sẽ trình bày chi tiết lý thuyết này theo chương trình Cánh Diều, giúp học sinh nắm vững kiến thức và áp dụng hiệu quả.
Định nghĩa: Căn bậc hai của một số thực a (với a ≥ 0) là số x sao cho x2 = a. Ký hiệu: √a.
Ví dụ: √9 = 3 vì 32 = 9.
Tính chất:
Định nghĩa: Căn bậc ba của một số thực a là số x sao cho x3 = a. Ký hiệu: 3√a.
Ví dụ:3√8 = 2 vì 23 = 8.
Tính chất:
Để so sánh các số thực sử dụng căn bậc hai và căn bậc ba, ta thường đưa chúng về cùng số mũ hoặc sử dụng tính chất đơn điệu của hàm số.
Ví dụ: So sánh √5 và 3√10.
Ta có: (√5)6 = 53 = 125 và (3√10)6 = 102 = 100.
Vì 125 > 100 nên √5 > 3√10.
Bài 1: Tính giá trị của biểu thức: √(16) + 3√27
Giải: √(16) = 4 và 3√27 = 3. Vậy √(16) + 3√27 = 4 + 3 = 7.
Bài 2: Rút gọn biểu thức: √ (x2 + 6x + 9) (với x ≥ -3)
Giải: √ (x2 + 6x + 9) = √ (x + 3)2 = |x + 3|. Vì x ≥ -3 nên x + 3 ≥ 0, do đó |x + 3| = x + 3.
Khi làm việc với căn bậc hai, cần chú ý đến điều kiện xác định của căn thức (căn thức phải lớn hơn hoặc bằng 0). Đối với căn bậc ba, không có điều kiện xác định vì căn bậc ba của mọi số thực đều tồn tại.
Việc nắm vững các tính chất của căn bậc hai và căn bậc ba sẽ giúp bạn giải quyết các bài toán một cách nhanh chóng và chính xác.
Lý thuyết về căn bậc hai và căn bậc ba được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và khoa học, như tính toán diện tích, thể tích, giải các bài toán hình học, và trong các lĩnh vực kỹ thuật.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết căn bậc hai và căn bậc ba của số thực Toán 9 Cánh Diều. Chúc bạn học tập tốt!