Chào mừng các em học sinh đến với bài giải chi tiết mục 3 trang 107 SGK Toán 9 tập 2 - Cánh diều tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập Toán 9.
Bài giải này được xây dựng bởi đội ngũ giáo viên giàu kinh nghiệm, đảm bảo tính chính xác và phù hợp với chương trình học.
Cho một hình cầu bán kính R và một cốc thuỷ tỉnh có dạng hình trụ với bán kính đáy là R, chiều cao là 2R. Đặt hình cầu nằm khít trong cốc hình trụ rồi đổ đầy nước vào cốc đó (Hình 36a). Nhấc nhẹ hình cầu ra khỏi cốc. Đo độ cao cột nước còn lại, ta thấy độ cao này chỉ bằng (frac{1}{3}) chiều cao của cốc (Hình 36b). Hãy cho biết thể tích của hình cầu bằng bao nhiêu phần thể tích của cốc hình trụ.
Đề bài
Trả lời câu hỏi Hoạt động 5 trang 107 SGK Toán 9 Cánh diều
Cho một hình cầu bán kính R và một cốc thuỷ tỉnh có dạng hình trụ với bán kính đáy là R, chiều cao là 2R.
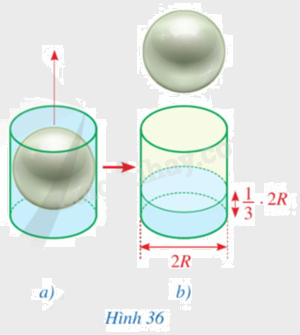
Đặt hình cầu nằm khít trong cốc hình trụ rồi đổ đầy nước vào cốc đó (Hình 36a). Nhấc nhẹ hình cầu ra khỏi cốc. Đo độ cao cột nước còn lại, ta thấy độ cao này chỉ bằng \(\frac{1}{3}\) chiều cao của cốc (Hình 36b). Hãy cho biết thể tích của hình cầu bằng bao nhiêu phần thể tích của cốc hình trụ.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính thể tích hình trụ để tích thể tích cốc và thể tích nước trong cốc.
Từ đó suy ra thể tích của hình cầu.
Lời giải chi tiết
Thể tích của cốc hình trụ là:
\(\pi .{R^2}.2R = 2\pi .{R^3}\)
Khi bỏ quả cầu ra thì độ cao nước còn lại bằng \(\frac{1}{3}\) chiều cao của cốc nên chiều cao nước là: \(\frac{1}{3}.2R = \frac{2}{3}R\).
Thể tích nước trong cốc là:
\(\pi .{R^2}.\frac{2}{3}R = \frac{2}{3}\pi {R^3}\).
Thể tích của cốc hình trụ chính là tổng thể tích của hình cầu và thể tích nước trong cốc.
Suy ra thể tích của hình cầu là:
\(2\pi {R^3} - \frac{2}{3}\pi {R^3} = \left( {2 - \frac{2}{3}} \right)\pi {R^3} = \frac{4}{3}\pi {R^3}\).
Vậy thể tích của hình cầu bằng \(\frac{{\frac{4}{3}\pi {R^3}}}{{2\pi {R^3}}} = \frac{2}{3}\) phần thể tích của hình trụ.
Mục 3 trang 107 SGK Toán 9 tập 2 - Cánh diều thường xoay quanh các bài toán liên quan đến hàm số bậc hai, bao gồm việc xác định hệ số, tìm đỉnh parabol, vẽ đồ thị hàm số và giải các bài toán ứng dụng thực tế. Việc nắm vững kiến thức về hàm số bậc hai là nền tảng quan trọng cho các chương trình học toán ở cấp độ cao hơn.
Để giải quyết các bài tập trong mục 3 trang 107, học sinh cần hiểu rõ các khái niệm sau:
Bài tập: Cho hàm số y = 2x2 - 4x + 1. Hãy tìm tọa độ đỉnh của parabol.
Giải:
Hệ số a = 2, b = -4, c = 1.
Tọa độ đỉnh I(xI, yI) được tính như sau:
xI = -b/2a = -(-4)/(2*2) = 1
yI = -Δ/4a = -((-4)2 - 4*2*1)/(4*2) = - (16 - 8)/8 = -1
Vậy tọa độ đỉnh của parabol là I(1, -1).
Ngoài SGK Toán 9 tập 2 - Cánh diều, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng với bài giải chi tiết và phương pháp giải bài tập được trình bày ở trên, các em học sinh sẽ tự tin hơn khi giải các bài tập mục 3 trang 107 SGK Toán 9 tập 2 - Cánh diều. Chúc các em học tập tốt!