Giải bài tập 1 trang 90 SGK Toán 9 tập 1 - Cánh diều

Chào mừng các em học sinh đến với lời giải chi tiết bài tập 1 trang 90 SGK Toán 9 tập 1 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi luôn cố gắng cung cấp những đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Bài tập 1 thuộc chương trình học Toán 9 tập 1, tập trung vào việc ôn tập và hệ thống hóa các kiến thức về hàm số bậc nhất. Việc giải bài tập này sẽ giúp các em củng cố lý thuyết và rèn luyện kỹ năng giải toán.

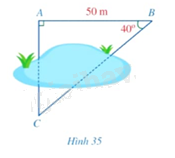
Hình 35 mô tả ba vị trí (A,B,C) là ba đỉnh của một tam giác vuông và không đo được trực tiếp các khoảng cách từ (C) đến (A) và từ (C) đến (B). Biết (AB = 50m), (widehat {ABC} = 40^circ ). Tính khoảng cách (CA) và (CB) (làm tròn kết quả đến hàng đơn vị của mét).

Đề bài

Hình 35 mô tả ba vị trí \(A,B,C\) là ba đỉnh của một tam giác vuông và không đo được trực tiếp các khoảng cách từ \(C\) đến \(A\) và từ \(C\) đến \(B\). Biết \(AB = 50m\), \(\widehat {ABC} = 40^\circ \). Tính khoảng cách \(CA\) và \(CB\) (làm tròn kết quả đến hàng đơn vị của mét).

Giải bài tập 1 trang 90 SGK Toán 9 tập 1 - Cánh diều 1

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài tập 1 trang 90 SGK Toán 9 tập 1 - Cánh diều 2

Dựa vào tỉ số lượng giác để giải bài toán.

Lời giải chi tiết

Xét tam giác \(ABC\) vuông tại \(A\), ta có:

+ \(AC = AB.{{\tan 40^\circ }} = 50{{\tan 40^\circ }} \approx 42\left( m \right)\).

+ \(BC = \frac{{AB}}{{\cos 40^\circ }} = \frac{{50}}{{\cos 40^\circ }} \approx 65\left( m \right)\).

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài tập 1 trang 90 SGK Toán 9 tập 1 - Cánh diều đặc sắc thuộc chuyên mục giải sgk toán 9 trên nền tảng toán math. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài tập 1 trang 90 SGK Toán 9 tập 1 - Cánh diều: Tổng quan và Phương pháp giải

Bài tập 1 trang 90 SGK Toán 9 tập 1 - Cánh diều là một bài tập quan trọng trong chương trình học Toán 9, giúp học sinh ôn tập và củng cố kiến thức về hàm số bậc nhất. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về hàm số, cách xác định hệ số góc và tung độ gốc, cũng như các phương pháp vẽ đồ thị hàm số.

Nội dung bài tập 1 trang 90 SGK Toán 9 tập 1 - Cánh diều

Bài tập 1 bao gồm các câu hỏi liên quan đến việc xác định hàm số bậc nhất, tìm hệ số góc và tung độ gốc, và vẽ đồ thị hàm số. Cụ thể, bài tập yêu cầu học sinh:

Xác định các hàm số bậc nhất trong một danh sách các hàm số cho trước.
Tìm hệ số góc và tung độ gốc của các hàm số bậc nhất.
Vẽ đồ thị của các hàm số bậc nhất.
Xác định các điểm thuộc đồ thị hàm số.

Phương pháp giải bài tập 1 trang 90 SGK Toán 9 tập 1 - Cánh diều

Để giải bài tập 1 trang 90 SGK Toán 9 tập 1 - Cánh diều, học sinh có thể áp dụng các phương pháp sau:

Xác định hàm số bậc nhất: Một hàm số được gọi là hàm số bậc nhất nếu nó có dạng y = ax + b, trong đó a và b là các số thực và a ≠ 0.
Tìm hệ số góc và tung độ gốc: Hệ số góc của hàm số bậc nhất y = ax + b là a, và tung độ gốc là b.
Vẽ đồ thị hàm số: Để vẽ đồ thị của hàm số bậc nhất y = ax + b, ta cần xác định hai điểm thuộc đồ thị, ví dụ như điểm cắt trục Oy (x = 0) và điểm cắt trục Ox (y = 0). Sau đó, ta nối hai điểm này lại với nhau để được đồ thị hàm số.
Xác định các điểm thuộc đồ thị hàm số: Để xác định xem một điểm có thuộc đồ thị hàm số y = ax + b hay không, ta thay tọa độ của điểm vào phương trình hàm số. Nếu phương trình nghiệm đúng, thì điểm đó thuộc đồ thị hàm số.

Ví dụ minh họa giải bài tập 1 trang 90 SGK Toán 9 tập 1 - Cánh diều

Ví dụ: Cho hàm số y = 2x - 1. Hãy xác định hệ số góc và tung độ gốc của hàm số, và vẽ đồ thị của hàm số.

Giải:

Hệ số góc của hàm số y = 2x - 1 là a = 2.
Tung độ gốc của hàm số y = 2x - 1 là b = -1.
Để vẽ đồ thị của hàm số y = 2x - 1, ta xác định hai điểm thuộc đồ thị:
- Khi x = 0, y = 2(0) - 1 = -1. Vậy điểm A(0; -1) thuộc đồ thị.
- Khi y = 0, 0 = 2x - 1 => x = 1/2. Vậy điểm B(1/2; 0) thuộc đồ thị.
Nối hai điểm A(0; -1) và B(1/2; 0) lại với nhau, ta được đồ thị của hàm số y = 2x - 1.

Lưu ý khi giải bài tập 1 trang 90 SGK Toán 9 tập 1 - Cánh diều

Khi giải bài tập 1 trang 90 SGK Toán 9 tập 1 - Cánh diều, học sinh cần lưu ý những điều sau:

Nắm vững các khái niệm cơ bản về hàm số bậc nhất.
Hiểu rõ cách xác định hệ số góc và tung độ gốc.
Thực hành vẽ đồ thị hàm số một cách thành thạo.
Kiểm tra lại kết quả sau khi giải bài tập.

Tổng kết

Bài tập 1 trang 90 SGK Toán 9 tập 1 - Cánh diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Bằng cách nắm vững các khái niệm cơ bản và áp dụng các phương pháp giải phù hợp, học sinh có thể giải bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tập tốt!