Chào mừng bạn đến với bài học lý thuyết về căn bậc hai trong chương trình Toán 9 Cánh diều. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về căn bậc hai, giúp bạn giải quyết các bài toán liên quan một cách hiệu quả.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất, các phép toán và ứng dụng của căn bậc hai trong thực tế.
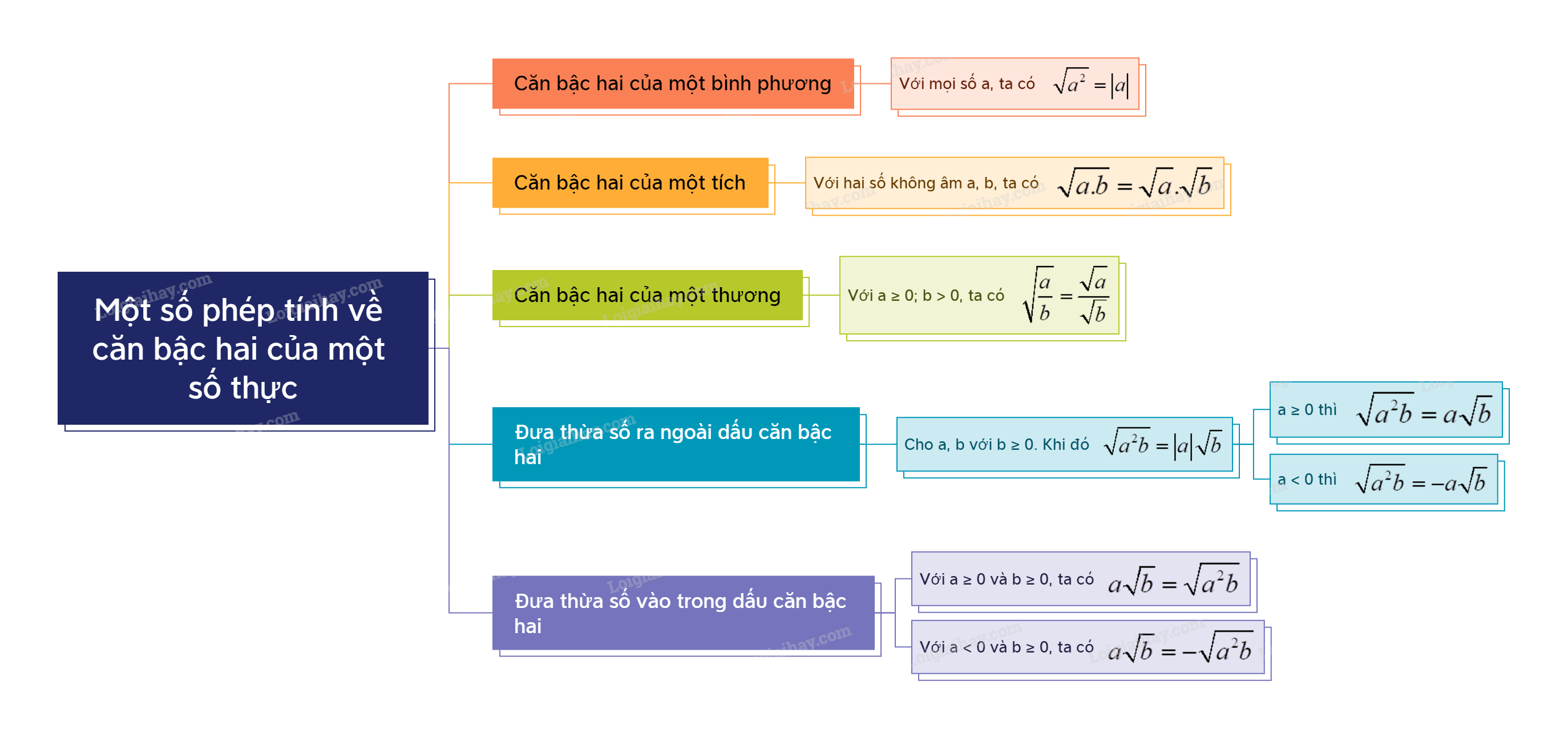
1. Căn bậc hai của một bình phương Với mọi số a, ta có: \(\sqrt {{a^2}} = \left| a \right|\).
1. Căn bậc hai của một bình phương
Với mọi số a, ta có: \(\sqrt {{a^2}} = \left| a \right|\). |
Ví dụ:
\(\sqrt {{{13}^2}} = \left| {13} \right| = 13\); \(\sqrt {{{\left( { - 8} \right)}^2}} = \left| { - 8} \right| = 8\).
2. Căn bậc hai của một tích
Với hai số không âm a, b, ta có: \(\sqrt {a.b} = \sqrt a .\sqrt b \). |
Chú ý: Quy tắc trên có thể mở rộng cho tích có nhiều thừa số không âm.
Ví dụ:
\(\sqrt {81.49} = \sqrt {81} .\sqrt {49} = 9.7 = 63\);
\(\sqrt {1,3} .\sqrt {10} .\sqrt {13} = \sqrt {1,3.10.13} = \sqrt {13.13} = \sqrt {{{13}^2}} = 13\).
3. Căn bậc hai của một thương
Với \(a \ge 0;b > 0\), ta có: \(\sqrt {\frac{a}{b}} = \frac{{\sqrt a }}{{\sqrt b }}\). |
Ví dụ:
\(\sqrt {\frac{4}{{25}}} = \frac{{\sqrt 4 }}{{\sqrt {25} }} = \frac{2}{5}\);
\(\frac{{\sqrt {216} }}{{\sqrt 6 }} = \sqrt {\frac{{216}}{6}} = \sqrt {36} = 6\).4. Đưa thừa số ra ngoài dấu căn bậc hai
Phép đưa thừa số ra ngoài dấu căn bậc hai
Cho hai số a, b với \(b \ge 0\). Khi đó \(\sqrt {{a^2}b} = \left| a \right|\sqrt b \). Cụ thể, ta có: - Nếu \(a \ge 0\) thì \(\sqrt {{a^2}b} = a\sqrt b \). - Nếu \(a < 0\) thì \(\sqrt {{a^2}b} = - a\sqrt b \). |
Ví dụ:
\(\sqrt {{7^2}.2} = 7\sqrt 2 \);
\(\sqrt {{{\left( { - 11} \right)}^2}.3} = \left| { - 11} \right|.\sqrt 3 = 11\sqrt 3 \).
5. Đưa thừa số vào trong dấu căn bậc hai
Phép đưa thừa số vào trong dấu căn bậc hai
- Với \(a \ge 0\) và \(b \ge 0\), ta có: \(a\sqrt b = \sqrt {{a^2}b} \). - Với \(a < 0\) và \(b \ge 0\), ta có: \(a\sqrt b = - \sqrt {{a^2}b} \). |
Ví dụ:
\(2\sqrt {\frac{1}{2}} = \sqrt {{2^2}.\frac{1}{2}} = \sqrt 2 \);
\(4\sqrt {\frac{7}{4}} - \sqrt {28} = \sqrt {{4^2}.\frac{7}{4}} - \sqrt {28} = \sqrt {4.7} - \sqrt {28} = \sqrt {28} - \sqrt {28} = 0\).
Căn bậc hai là một khái niệm quan trọng trong toán học, đặc biệt là trong chương trình Toán 9. Hiểu rõ lý thuyết về căn bậc hai sẽ giúp học sinh giải quyết các bài toán liên quan một cách chính xác và hiệu quả. Bài viết này sẽ trình bày chi tiết lý thuyết về căn bậc hai của một số thực, theo chương trình Toán 9 Cánh diều.
Với số thực a không âm (a ≥ 0), căn bậc hai của a là số x sao cho x2 = a.
Ký hiệu: √a
Ví dụ: √9 = 3 vì 32 = 9.
Căn bậc hai của một số thực chỉ xác định khi số đó không âm. Tức là, biểu thức √a chỉ có nghĩa khi a ≥ 0.
Để rút gọn biểu thức chứa căn bậc hai, ta cần phân tích số dưới dấu căn thành tích của các thừa số nguyên tố, sau đó đưa các thừa số có số mũ chẵn ra ngoài dấu căn.
Ví dụ: √18 = √(9 * 2) = √9 * √2 = 3√2
Căn bậc hai chỉ có thể cộng hoặc trừ với các căn bậc hai đồng dạng (tức là có cùng phần dưới dấu căn).
Ví dụ: 2√3 + 3√3 = 5√3
Để nhân hoặc chia các căn bậc hai, ta áp dụng các tính chất đã nêu ở trên.
Ví dụ: √2 * √3 = √6
√8 / √2 = √(8/2) = √4 = 2
Để so sánh hai số thực a và b (với a ≥ 0, b ≥ 0), ta có thể so sánh căn bậc hai của chúng.
Nếu √a < √b thì a < b.
Giải:
Căn bậc hai có nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và quan trọng về lý thuyết căn bậc hai của một số thực Toán 9 Cánh diều. Chúc bạn học tập tốt!