Chào mừng bạn đến với bài học lý thuyết Hình trụ Toán 9 Cánh diều tại giaitoan.edu.vn! Bài viết này sẽ cung cấp cho bạn một cách đầy đủ và dễ hiểu nhất về các khái niệm, định lý và công thức liên quan đến hình trụ, giúp bạn tự tin giải quyết các bài tập trong chương trình học.
Chúng ta sẽ cùng nhau khám phá cấu tạo, các yếu tố của hình trụ, cách tính diện tích xung quanh, diện tích toàn phần và thể tích của hình trụ. Đồng thời, bài viết cũng sẽ giới thiệu các bài tập minh họa để bạn có thể áp dụng kiến thức đã học vào thực tế.
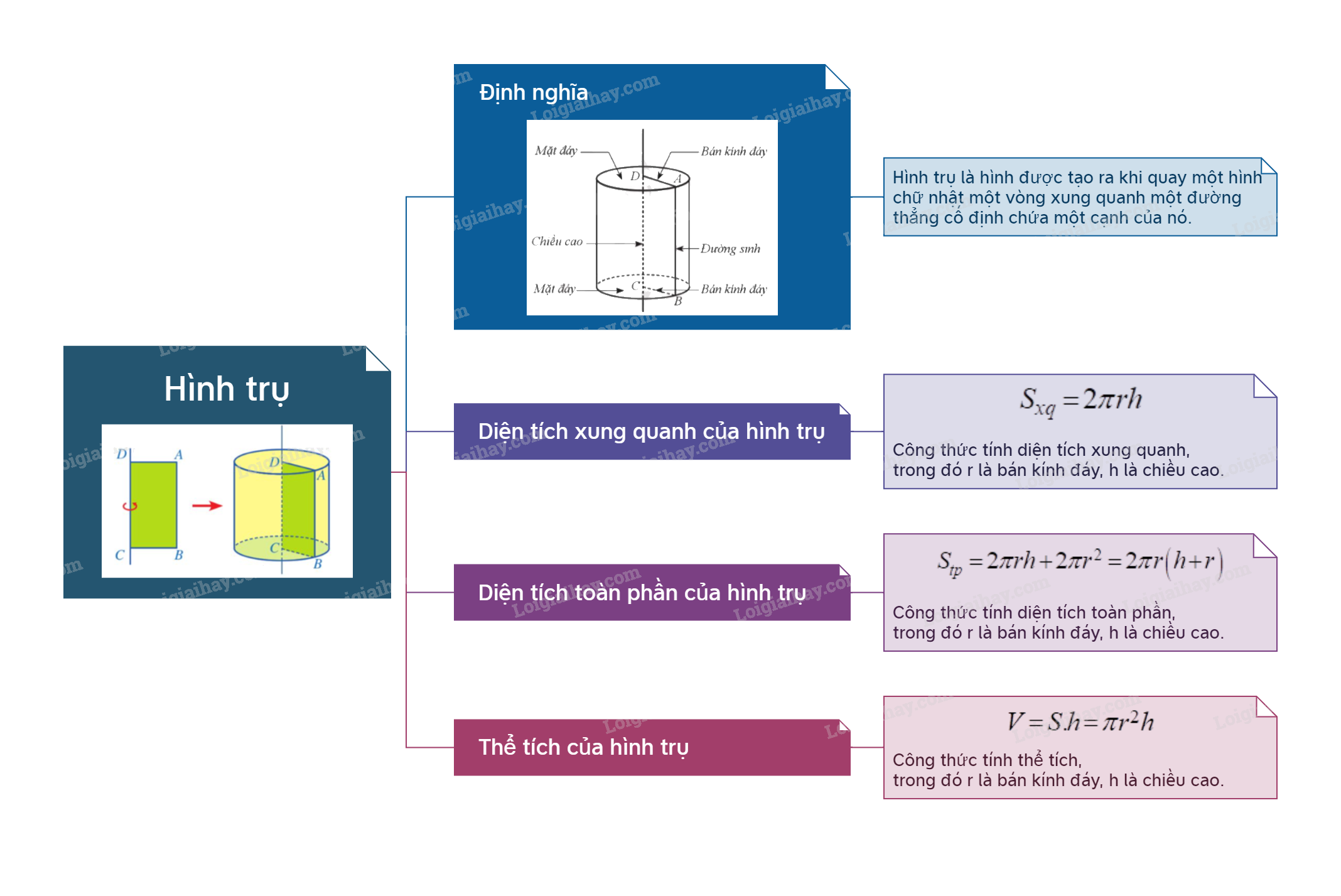
1. Hình trụ Định nghĩa Hình trụ là hình được tạo ra khi quay một hình chữ nhật một vòng xung quanh một đường thẳng cố định chứa một cạnh của nó.
1. Hình trụ
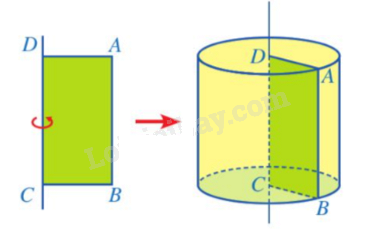
Định nghĩa
Hình trụ là hình được tạo ra khi quay một hình chữ nhật một vòng xung quanh một đường thẳng cố định chứa một cạnh của nó. |
Ví dụ:
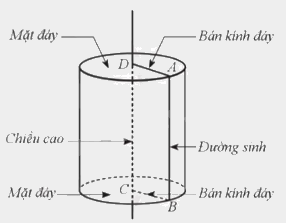
Hình trụ trên có:
- Hình tròn tâm D bán kính DA và hình tròn tâm C bán kính CB là hai mặt đáy;
hai mặt đáy của hình trụ bằng nhau và nằm trong hai mặt phẳng song song;
- Độ dài cạnh DA được gọi là bán kính đáy;
- Độ dài cạnh CD được gọi là chiều cao;
- Cạnh AB quét nên mặt xung quanh của hình trụ, mỗi vị trí của cạnh AB được gọi là một đường sinh; độ dài đường sinh bằng chiều cao của hình trụ.
2. Diện tích xung quanh của hình trụ
Diện tích xung quanh của hình trụ
Diện tích xung quanh \({S_{xq}}\) của hình trụ có bán kính đáy r và chiều cao h là: \({S_{xq}} = 2\pi rh\). |
Diện tích toàn phần của hình trụ
Diện tích toàn phần \({S_{tp}}\) bằng tổng của diện tích xung quanh và diện tích hai đáy của hình trụ: \({S_{tp}} = 2\pi rh + 2\pi {r^2} = 2\pi r\left( {h + r} \right)\) |
Ví dụ:
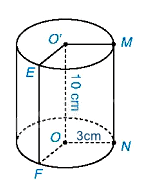
Diện tích xung quanh của hình trụ là:
\({S_{xq}} = 2\pi rh = 2\pi .3.10 = 60\pi \left( {c{m^2}} \right)\)
3. Thể tích của hình trụ
Thể tích V của hình trụ có bán kính đáy r và chiều cao h là: \(V = S.h = \pi {r^2}h\) (S là diện tích đáy của hình trụ).
|
Ví dụ:
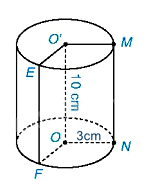
Diện tích đáy là:
\(S = \pi {r^2} = \pi {.3^2} = 9\pi \left( {c{m^2}} \right)\)
Thể tích của hình trụ là:
\(V = S.h = 9\pi .10 = 90\pi \left( {c{m^3}} \right)\)
Hình trụ là một hình khối hình học được tạo thành bởi hai hình tròn bằng nhau, song song với nhau và một mặt bên là mặt xung quanh của hình trụ. Hai hình tròn này được gọi là hai đáy của hình trụ.
Diện tích xung quanh của hình trụ được tính bằng công thức: Sxq = 2πrh, trong đó:
Diện tích toàn phần của hình trụ được tính bằng công thức: Stp = Sxq + 2Sđáy = 2πrh + 2πr2, trong đó:
Thể tích của hình trụ được tính bằng công thức: V = πr2h, trong đó:
Bài 1: Một hình trụ có bán kính đáy là 5cm và chiều cao là 10cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình trụ đó.
Giải:
Bài 2: Một hình trụ có thể tích là 1570cm3 và chiều cao là 10cm. Tính bán kính đáy của hình trụ đó.
Giải:
V = πr2h => r2 = V / (πh) = 1570 / (3.14159 * 10) = 50 => r = √50 ≈ 7.07cm
Lý thuyết về hình trụ có nhiều ứng dụng trong thực tế, ví dụ như tính thể tích của các vật thể hình trụ như lon nước, ống nước, cột trụ,... Ngoài ra, kiến thức về hình trụ còn là nền tảng để học các hình khối hình học khác phức tạp hơn.
Để nắm vững kiến thức về hình trụ, bạn nên luyện tập thêm nhiều bài tập khác nhau. Bạn có thể tìm thấy các bài tập này trong sách giáo khoa, sách bài tập hoặc trên các trang web học toán online như giaitoan.edu.vn.
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về lý thuyết Hình trụ Toán 9 Cánh diều. Chúc bạn học tập tốt!