Chào mừng bạn đến với bài học về lý thuyết Tiếp tuyến của đường tròn trong chương trình Toán 9 Cánh diều tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về tiếp tuyến, giúp bạn giải quyết các bài toán liên quan một cách hiệu quả.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất của tiếp tuyến, các định lý liên quan và cách áp dụng chúng vào giải bài tập. Hãy bắt đầu ngay thôi!
1. Nhận biết tiếp tuyến của đường tròn Nhận xét: Nếu một đường thẳng là tiếp tuyến của một đường tròn thì đường thẳng đó vuông góc với bán kính đi qua tiếp điểm.
1. Nhận biết tiếp tuyến của đường tròn
Nhận xét: Nếu một đường thẳng là tiếp tuyến của một đường tròn thì đường thẳng đó vuông góc với bán kính đi qua tiếp điểm.
Dấu hiệu nhận biết tiếp tuyến
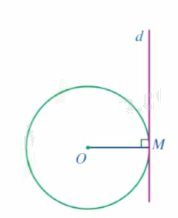
Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là tiếp tuyến của đường tròn. |
2. Tính chất của hai tiếp tuyến cắt nhau
Định lí
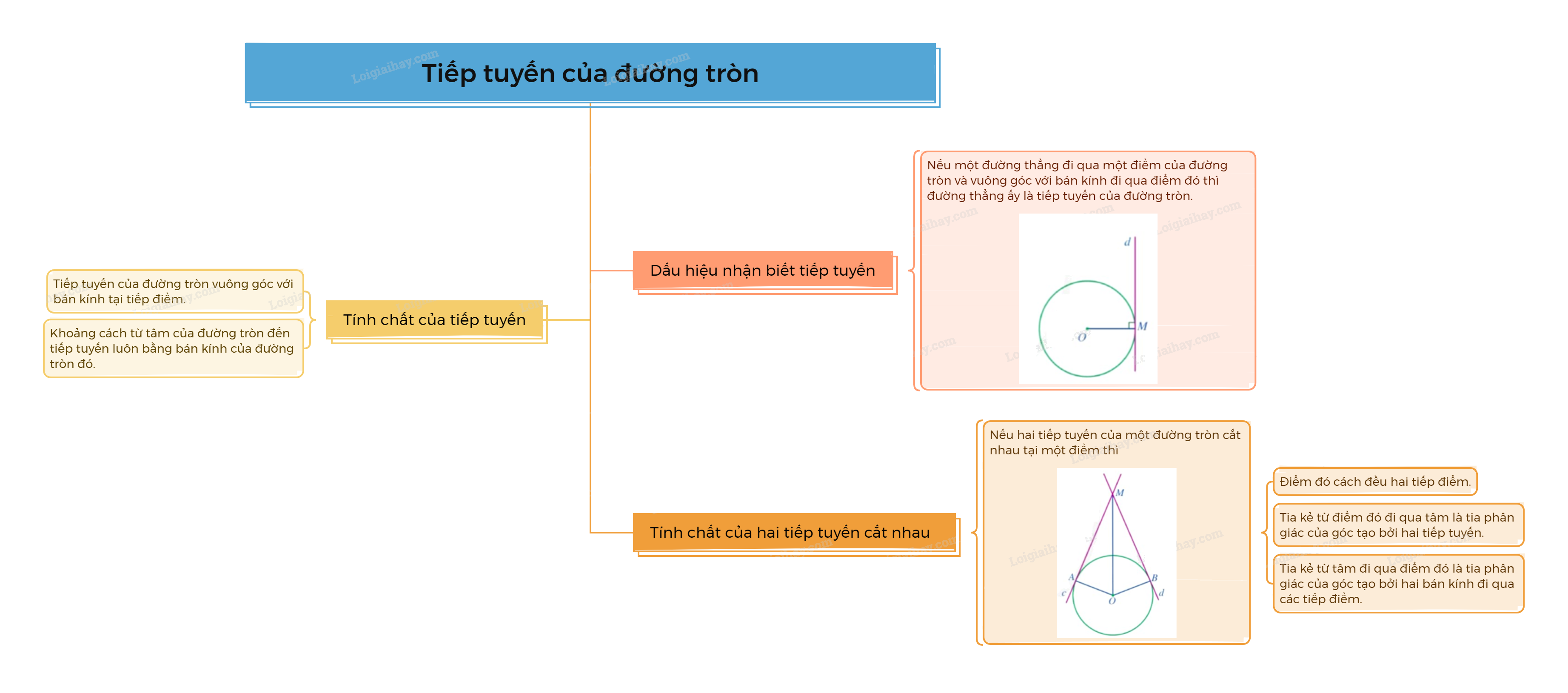
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì: - Điểm đó cách đều hai tiếp điểm. - Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến. - Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
|
Ví dụ: Cho đường tròn (O), B, C \( \in \) (O). Tiếp tuyến của (O) tại B và C cắt nhau tại A.
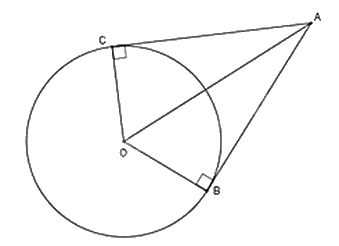
Khi đó:
- AB = AC
- Tia AO là tia phân giác của \(\widehat {BAC}\).
- Tia OA là tia phân giác của \(\widehat {BOC}\).
Tiếp tuyến của đường tròn là một khái niệm quan trọng trong hình học lớp 9, đặc biệt trong chương trình Toán 9 Cánh Diều. Hiểu rõ lý thuyết này là nền tảng để giải quyết các bài toán liên quan đến đường tròn một cách chính xác và hiệu quả.
Tiếp tuyến của một đường tròn (O) là một đường thẳng có đúng một điểm chung với đường tròn đó. Điểm chung này được gọi là tiếp điểm.
Ví dụ: Đường thẳng d là tiếp tuyến của đường tròn (O) tại điểm A nếu d chỉ đi qua A và không cắt đường tròn tại bất kỳ điểm nào khác.
Định lý 1: Nếu một đường thẳng là tiếp tuyến của một đường tròn tại một điểm, thì đường thẳng đó vuông góc với bán kính tại điểm đó.
Chứng minh: (Chứng minh được dựa trên các định lý về góc và đường thẳng vuông góc)
Hệ quả: Bán kính nối từ tâm đường tròn đến tiếp điểm vuông góc với tiếp tuyến tại tiếp điểm.
Định lý 2: Nếu một đường thẳng đi qua một điểm nằm ngoài đường tròn và cắt đường tròn tại hai điểm, thì đường thẳng đó là một đường thẳng cắt.
Định lý 3: Nếu một đường thẳng đi qua một điểm nằm ngoài đường tròn và chỉ có một điểm chung với đường tròn, thì đường thẳng đó là một tiếp tuyến.
Định lý 1: Từ một điểm nằm ngoài đường tròn, chỉ có thể vẽ được hai tiếp tuyến đến đường tròn đó.
Định lý 2: Độ dài hai đoạn thẳng kẻ từ một điểm nằm ngoài đường tròn đến hai tiếp điểm bằng nhau.
Chứng minh: Xét hai tiếp tuyến OA và OB của đường tròn (O) từ điểm A nằm ngoài đường tròn. Ta có OA = OB (bán kính), góc OAB = góc OBA (tính chất hai tiếp tuyến kẻ từ một điểm). Do đó, tam giác OAB cân tại O, suy ra AB = AB.
Bài 1: Cho đường tròn (O) đường kính 10cm. Từ một điểm A nằm ngoài đường tròn, kẻ hai tiếp tuyến AB và AC đến đường tròn (B và C là tiếp điểm). Biết OA = 13cm. Tính độ dài AB.
Giải: Vì AB là tiếp tuyến của đường tròn (O) tại B, nên góc OBA = 90 độ. Áp dụng định lý Pitago vào tam giác OBA, ta có: AB2 = OA2 - OB2 = 132 - 52 = 169 - 25 = 144. Suy ra AB = 12cm.
Bài 2: Cho đường tròn (O) và một điểm A nằm ngoài đường tròn. Kẻ tiếp tuyến AB đến đường tròn (B là tiếp điểm). Kẻ đường thẳng d đi qua A cắt đường tròn tại hai điểm C và D. Chứng minh rằng AB2 = AC.AD.
Giải: (Chứng minh dựa trên các tam giác đồng dạng)
Lý thuyết tiếp tuyến của đường tròn có nhiều ứng dụng trong thực tế, ví dụ như trong việc thiết kế bánh xe, hệ thống truyền động, hoặc trong các bài toán liên quan đến quang học.
Việc nắm vững lý thuyết này không chỉ giúp bạn giải quyết các bài toán trong sách giáo khoa mà còn mở ra khả năng ứng dụng kiến thức vào các lĩnh vực khác.
Bài học về lý thuyết Tiếp tuyến của đường tròn Toán 9 Cánh Diều đã cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất. Hãy luyện tập thêm nhiều bài tập để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.
Chúc bạn học tốt!