Phương trình bậc hai một ẩn là một trong những kiến thức trọng tâm của chương trình Toán 9 Cánh Diều. Việc nắm vững lý thuyết và phương pháp giải phương trình bậc hai là nền tảng quan trọng để học tốt các kiến thức toán học ở các lớp trên.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu về lý thuyết phương trình bậc hai một ẩn, kèm theo các bài tập vận dụng đa dạng giúp bạn hiểu sâu và nắm vững kiến thức.
1. Định nghĩa phương trình bậc hai một ẩn Phương trình bậc hai một ẩn (nói gọn là phương trình bậc hai) là phương trình có dạng \(a{x^2} + bx + c = 0\), trong đó x là ẩn; a, b, c là những số cho trước gọi là các hệ số và \(a \ne 0\).
1. Định nghĩa phương trình bậc hai một ẩn
Phương trình bậc hai một ẩn (nói gọn là phương trình bậc hai) là phương trình có dạng \(a{x^2} + bx + c = 0\), trong đó x là ẩn; a, b, c là những số cho trước gọi là các hệ số và \(a \ne 0\). |
Ví dụ: Phương trình \(2{x^2} - 3x + 1 = 0\) là phương trình bậc hai với \(a = 2;b = - 3;c = 1\).
Phương trình \({x^2} - 3 = 0\) là phương trình bậc hai với \(a = 1,b = 0,c = - 3\).
Phương trình \(0{x^2} - 2x - 3 = 0\) không là phương trình bậc hai vì \(a = 0\).
2. Giải phương trình
Giải phương trình bậc hai \({\left( {x - n} \right)^2} = m\)
Khi m > 0, ta có: \({\left( {x - n} \right)^2} = m\) \(x - n = \sqrt m \) hoặc \(x - n = - \sqrt m \) \(x = n + \sqrt m \) hoặc \(x = n - \sqrt m \). Như vậy, phương trình có hai nghiệm là \({x_1} = n + \sqrt m \) và \({x_2} = n - \sqrt m \). |
Ví dụ: Giải phương trình \({\left( {x - 1} \right)^2} = 3\)
Ta có: \({\left( {x - 1} \right)^2} = 3\)
\(x - 1 = \sqrt 3 \) hoặc \(x - 1 = - \sqrt 3 \)
\(x = 1 + \sqrt 3 \) hoặc \(x = 1 - \sqrt 3 \).
Vậy phương trình đã cho có hai nghiệm là \({x_1} = 1 + \sqrt 3 \) và \({x_2} = 1 - \sqrt 3 \).
3. Công thức nghiệm của phương trình bậc hai
Công thức nghiệm của phương trình bậc hai:
Xét phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) và biệt thức \(\Delta = {b^2} - 4ac\). - Nếu \(\Delta > 0\) thì phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - b + \sqrt \Delta }}{{2a}};{x_2} = \frac{{ - b - \sqrt \Delta }}{{2a}}\). - Nếu \(\Delta = 0\) thì phương trình có nghiệm kép \({x_1} = {x_2} = - \frac{b}{{2a}}\). - Nếu \(\Delta < 0\) thì phương trình vô nghiệm. |
Ví dụ: Giải phương trình \({x^2} - 7x - 8 = 0\).
Ta có: \(a = 1,b = - 7,c = - 8\).
\(\Delta = {b^2} - 4ac = {\left( { - 7} \right)^2} - 4.1.\left( { - 8} \right) = 81 > 0\).
Vậy phương trình có hai nghiệm phân biệt là
\({x_1} = \frac{{ - \left( { - 7} \right) + \sqrt {81} }}{{2.1}} = 8;{x_2} = \frac{{ - \left( { - 7} \right) - \sqrt {81} }}{{2.1}} = - 1\).
Công thức nghiệm thu gọn của phương trình bậc hai:
Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\), với \(b = 2b'\) và \(\Delta ' = b{'^2} - ac\). - Nếu \(\Delta ' > 0\) thì phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - b' + \sqrt {\Delta '} }}{a};{x_2} = \frac{{ - b' - \sqrt {\Delta '} }}{a}\). - Nếu \(\Delta ' = 0\) thì phương trình có nghiệm kép \({x_1} = {x_2} = - \frac{{b'}}{a}\). - Nếu \(\Delta ' < 0\) thì phương trình vô nghiệm. |
Ví dụ: Giải phương trình \(7{x^2} - 12x + 5 = 0\).
Ta có: \(a = 7,b' = - 6,c = 5\).
\(\Delta ' = b{'^2} - ac = {\left( { - 6} \right)^2} - 7.5 = 1 > 0\).
Vậy phương trình có hai nghiệm phân biệt là
\({x_1} = \frac{{ - \left( { - 6} \right) + 1}}{7} = 1;{x_2} = \frac{{ - \left( { - 6} \right) - 1}}{7} = \frac{5}{7}\).
4. Ứng dụng của phương trình bậc hai một ẩn
Phương trình bậc hai một ẩn giúp chúng ta giải quyết nhiều vấn đề trong toán học cũng như trong thực tiễn.
Để giải bài toán bằng cách lập phương trình bậc hai, ta có thể làm như sau:
Bước 1: Lập phương trình bậc hai - Chọn ẩn và đặt điều kiện cho ẩn số - Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết - Lập phương trình bậc hai biểu thị mối quan hệ giữa các đại lượng Bước 2. Giải phương trình bậc hai Bước 3. Kết luận - Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn, nghiệm nào không thỏa mãn điều kiện của ẩn. - Đưa ra câu trả lời cho bài toán. |
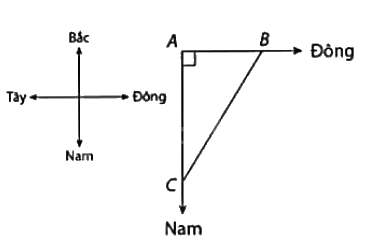
Ví dụ: Một ca nô xuất phát từ một bến và có chuyển động thẳng theo hướng Đông. Cùng lúc đó, một tàu thủy rời bến và chuyển động thẳng theo hướng Nam với tốc độ lớn hơn tốc độ của ca nô 8km/h. Tính tốc độ của ca nô, biết sau một giờ kể từ lúc xuất phát, khoảng cách giữa ca nô với tàu thủy là 40km.
Lời giải:
Gọi tốc độ của ca nô là \(x\left( {km/h} \right)\left( {x > 0} \right)\).
Tốc độ của tàu thủy là \(x + 8\left( {km/h} \right)\).
Gọi A là vị trí của bến, gọi B, C lần lượt là vị trí của ca nô và tàu thủy sau khi rời bến 1 giờ (như hình vẽ).
Quãng đường ca nô đi được sau 1 giờ là:
\(AB = x.1 = x\left( {km} \right)\)
Quãng đường tàu thủy đi được sau 1 giờ là:
\(AC = \left( {x + 8} \right).1 = x + 8\left( {km} \right)\)
Ca nô và tày thủy chuyển động theo hai hướng vuông góc với nhau nên tam giác ABC vuông tại A.
Ta có: \(A{B^2} + A{C^2} = B{C^2}\) (định lí Pythagore).
\(\begin{array}{l}{x^2} + {\left( {x + 8} \right)^2} - {40^2}\\{x^2} + {x^2} + 16x + 64 = 1600\\2{x^2} + 16x - 1536 = 0\\{x^2} + 8x - 768 = 0\end{array}\)
Ta có: \(\Delta ' = {4^2} + 768 = 784,\sqrt {\Delta '} = 28\).
Suy ra phương trình có hai nghiệm phân biệt:
\({x_1} = \frac{{ - 4 - 28}}{1} = - 32\) (loại); \({x_2} = \frac{{ - 4 + 28}}{1} = 24\) (thỏa mãn điều kiện).
Vậy tốc độ của ca nô là \(24km/h\).
5. Tìm nghiệm của phương trình bậc hai bằng máy tính cầm tay
Sử dụng máy tính cầm tay, ta có thể dễ dạng tìm nghiệm của các phương trình bậc hai.
Bước 1. Ta sử dụng loại máy tính cầm tay (MTCT) có chức năng này (có phím MODE/MENU).
- Đối với máy Fx-570VN PLUS, ta bấm phím MODE rồi bấm phím 5 rồi bấm phím 3 để chuyển về chế độ giải phương trình bậc hai.

- Đối với máy Fx-580VNX, ta bấm MENU rồi bấm phím 9 để chọn tính năng Equation/Func (Ptrình/HệPtrình).
Bấm phím 2 để chọn Polynomial Degree
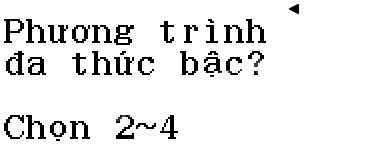
Cuối cùng, bấm phím 2 để giải phương trình bậc hai
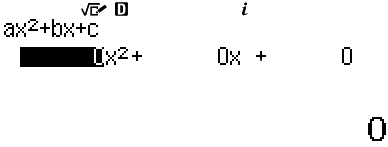
Bước 2. Ta nhập các hệ số \(a,b,c\) bằng cách bấm
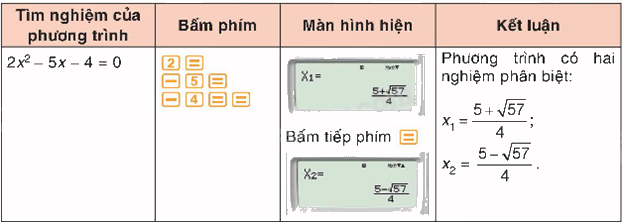
Đối với phương trình bậc hai có nghiệm kép, ta nhận được kết quả hiển thị trên màn hình như sau:

Đối với phương trình bậc hai vô nghiệm, ta nhận được kết quả hiển thị trên màn hình như sau:

Phương trình bậc hai một ẩn là phương trình có dạng tổng quát: ax² + bx + c = 0, trong đó a, b, c là các số thực và a ≠ 0. Đây là một trong những chủ đề quan trọng trong chương trình Toán 9, đặc biệt là theo sách Cánh Diều. Việc hiểu rõ lý thuyết và các phương pháp giải phương trình bậc hai là nền tảng vững chắc cho việc học tập các kiến thức toán học nâng cao hơn.
Như đã đề cập, phương trình bậc hai một ẩn có dạng ax² + bx + c = 0. Các hệ số a, b, c đóng vai trò quan trọng trong việc xác định tính chất và phương pháp giải của phương trình.
Trong quá trình giải phương trình bậc hai, chúng ta thường gặp một số dạng đặc biệt:
Để xác định số nghiệm của phương trình bậc hai, chúng ta sử dụng khái niệm delta (Δ), được tính bằng công thức:
Δ = b² - 4ac
Dựa vào giá trị của Δ, ta có thể kết luận về số nghiệm của phương trình:
Công thức nghiệm tổng quát của phương trình bậc hai ax² + bx + c = 0 là:
x = (-b ± √Δ) / 2a
Trong đó:
Phương trình bậc hai có rất nhiều ứng dụng trong thực tế, ví dụ như:
Để củng cố kiến thức về lý thuyết phương trình bậc hai, hãy cùng giải một số bài tập sau:
Lý thuyết phương trình bậc hai một ẩn là một phần quan trọng của chương trình Toán 9 Cánh Diều. Việc nắm vững lý thuyết, công thức và các phương pháp giải phương trình bậc hai sẽ giúp bạn tự tin giải quyết các bài toán liên quan và xây dựng nền tảng vững chắc cho việc học tập các kiến thức toán học nâng cao hơn. Hãy luyện tập thường xuyên để đạt kết quả tốt nhất!