Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải chi tiết và dễ hiểu cho bài tập 4 trang 100 SGK Toán 9 tập 1, chương trình Cánh diều.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho đường tròn (left( {O;R} right)) và dây(AB = R). Tính số đo góc (AOB).
Đề bài
Cho đường tròn \(\left( {O;R} \right)\) và dây \(AB = R\). Tính số đo góc \(AOB\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào tính chất của tam giác để tính.
Lời giải chi tiết
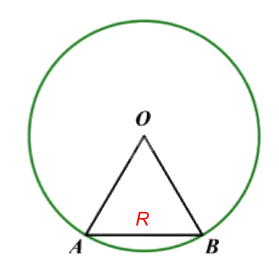
Do \(OA = OB = AB = R\) từ đó suy ra \(\Delta OAB\) là tam giác đều. Vậy \(\widehat {AOB} = 60^\circ \).
Bài tập 4 trang 100 SGK Toán 9 tập 1 - Cánh diều thuộc chương trình đại số, tập trung vào việc giải phương trình bậc hai một ẩn. Đây là một dạng bài tập quan trọng, thường xuyên xuất hiện trong các bài kiểm tra và thi cử. Việc nắm vững phương pháp giải phương trình bậc hai là nền tảng để học các kiến thức toán học nâng cao hơn.
Bài tập 4 bao gồm một số phương trình bậc hai với các hệ số khác nhau. Các phương trình này có thể được giải bằng nhiều phương pháp khác nhau, tùy thuộc vào dạng của phương trình. Các phương pháp thường được sử dụng bao gồm:
Lời giải:
Phương trình x2 - 5x + 6 = 0 có thể được phân tích thành nhân tử như sau:
(x - 2)(x - 3) = 0
Từ đó, ta có hai nghiệm:
Vậy, phương trình có hai nghiệm là x = 2 và x = 3.
Lời giải:
Phương trình 2x2 + 5x - 3 = 0 là một phương trình bậc hai tổng quát. Ta có thể sử dụng công thức nghiệm để giải phương trình này:
x = (-b ± √(b2 - 4ac)) / 2a
Trong đó, a = 2, b = 5, c = -3.
Thay các giá trị vào công thức, ta được:
x = (-5 ± √(52 - 4 * 2 * (-3))) / (2 * 2)
x = (-5 ± √(25 + 24)) / 4
x = (-5 ± √49) / 4
x = (-5 ± 7) / 4
Từ đó, ta có hai nghiệm:
Vậy, phương trình có hai nghiệm là x = 1/2 và x = -3.
Lời giải:
Phương trình x2 - 4x + 4 = 0 có thể được viết lại dưới dạng:
(x - 2)2 = 0
Từ đó, ta có nghiệm duy nhất:
x - 2 = 0 => x = 2
Vậy, phương trình có nghiệm duy nhất là x = 2.
Việc giải phương trình bậc hai có nhiều ứng dụng trong thực tế, chẳng hạn như:
Hy vọng bài viết này đã giúp các em hiểu rõ hơn về cách giải bài tập 4 trang 100 SGK Toán 9 tập 1 - Cánh diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!