Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3 trang 76 và 77 sách giáo khoa Toán 9 tập 2 - Cánh diều.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho hình chữ nhật ABCD, AC cắt BD tại O (Hình 24). Đặt R = OA và vẽ đường tròn (O; R). Các điểm A, B, C, D có thuộc (O; R) hay không?
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 4 trang 77SGK Toán 9 Cánh diều
Tính tỉ số giữa chu vi của một hình vuông và chu vi của một đường tròn ngoại tiếp hình vuông đó.
Phương pháp giải:
Tính tỉ số giữa chu vi của một hình vuông và chu vi của một đường tròn ngoại tiếp hình vuông đó là: chu vi hình vuông : chu vi đường tròn.
Lời giải chi tiết:
Giả sử hình vuông có cạnh là a, thì bán kính đường tròn ngoại tiếp hình vuông đó là \(\frac{{\sqrt 2 a}}{2}.\)
Chu vi hình vuông là 4a, chu vi của đường tròn ngoại tiếp là \(2\frac{{\sqrt 2 a}}{2}\pi = \sqrt 2 a\pi .\)
Tính tỉ số giữa chu vi của một hình vuông và chu vi của một đường tròn ngoại tiếp hình vuông đó là: \(\frac{{4a}}{{\sqrt 2 a\pi }} = \frac{{2\sqrt 2 }}{\pi }.\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 77SGK Toán 9 Cánh diều
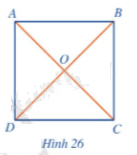
Cho hình vuông ABCD, ACcắt BDtại (O) (Hình 26).
a) Mỗi đường chéo của hình vuông ABCD có phải là đường kính của đường tròn ngoại tiếp hình vuông đó hay không?
b) Cho biết AB = a, tính OA theo a.
Phương pháp giải:
a) Mỗi hình vuông là một hình chữ nhật.
b) Áp dụng định lý Pytago trong tam giác OAB.
Lời giải chi tiết:
a) Vì hình vuông cũng là một hình chữ nhật nên mỗi đường chéo của hình vuông cũng là đường kính của đường tròn ngoại tiếp hình vuông đó.
b) Vì ABCD là hình vuông nên \(AC \bot BD\) hay \(\widehat {AOB} = 90^\circ \) và OA = OB.
Xét tam giác OAB vuông tại O, ta có:
\(\begin{array}{l}O{A^2} + O{B^2} = A{B^2}\\2O{A^2} = {a^2}\\OA = \frac{{\sqrt 2 a}}{2}.\end{array}\)
Vậy \(OA = \frac{{\sqrt 2 a}}{2}.\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 77SGK Toán 9 Cánh diều
Người ta làm một logo có dạng hình tròn, trong đó có một hình chữ nhật nội tiếp đường tròn với chiều dài và chiều rộng lần lượt là 8cm và 6cm. Hình chữ nhật được tô màu xanh còn phần khác của logo được tô màu đỏ. Tính diện tích phần được tô màu đỏ.
Phương pháp giải:
Diện tích tô màu đỏ = diện tích hình tròn – diện tích hình chữ nhật.
Lời giải chi tiết:
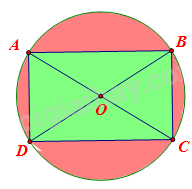
Giả sử ta có hình chữ nhật ABCD nội tiếp đường tròn tâm (O).
Suy ra bán kính đường tròn là OC, đường kính AC.
Hình chữ nhật ABCD có chiều dài AB = 8cm, chiều rộng BC = 6cm. Áp dụng định lý Pytago trong tam giác vuông ABC có:
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{8^2} + {6^2}} = 10cm.\)
Do đó \(R = OC = \frac{{AC}}{2} = \frac{{10}}{2} = 5cm.\)
Diện tích hình tròn là: \(\pi {R^2} = \pi {.5^2} = 25\pi (c{m^2}).\)
Diện tích hình chữ nhật là: \(8.6 = 48(c{m^2}).\)
Diện tích phần tô màu đỏ là: \(25\pi - 48 \approx 30,5(c{m^2})\) (với \(\pi \approx 3,14\)).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 76 SGK Toán 9 Cánh diều
Cho hình chữ nhật ABCD, AC cắt BD tại O (Hình 24). Đặt R = OA và vẽ đường tròn (O; R). Các điểm A, B, C, D có thuộc (O; R) hay không?
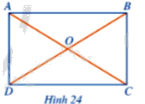
Phương pháp giải:
Áp dụng tính chất: Hình chữ nhật có 2 đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường” để chứng minh AO = CO = OB = OD = R.
Lời giải chi tiết:
Do ABCD là hình chữ nhật nên 2 đường chéo cắt nhau tại trung điểm O của mỗi đường, do đó AO = CO= \(\frac{1}{2}AC\) và OB = OD = \(\frac{1}{2}BD\). Mà AC = BD (tính chất hình chữ nhật)
Suy ra AO = CO = OB = OD = R.
Vậy các điểm A, B, C, D thuộc (O; R).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 76 SGK Toán 9 Cánh diều
Cho hình chữ nhật ABCD, AC cắt BD tại O (Hình 24). Đặt R = OA và vẽ đường tròn (O; R). Các điểm A, B, C, D có thuộc (O; R) hay không?
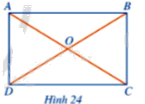
Phương pháp giải:
Áp dụng tính chất: Hình chữ nhật có 2 đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường” để chứng minh AO = CO = OB = OD = R.
Lời giải chi tiết:
Do ABCD là hình chữ nhật nên 2 đường chéo cắt nhau tại trung điểm O của mỗi đường, do đó AO = CO= \(\frac{1}{2}AC\) và OB = OD = \(\frac{1}{2}BD\). Mà AC = BD (tính chất hình chữ nhật)
Suy ra AO = CO = OB = OD = R.
Vậy các điểm A, B, C, D thuộc (O; R).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 3 trang 77SGK Toán 9 Cánh diều
Người ta làm một logo có dạng hình tròn, trong đó có một hình chữ nhật nội tiếp đường tròn với chiều dài và chiều rộng lần lượt là 8cm và 6cm. Hình chữ nhật được tô màu xanh còn phần khác của logo được tô màu đỏ. Tính diện tích phần được tô màu đỏ.
Phương pháp giải:
Diện tích tô màu đỏ = diện tích hình tròn – diện tích hình chữ nhật.
Lời giải chi tiết:
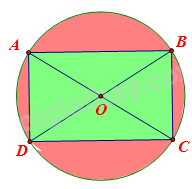
Giả sử ta có hình chữ nhật ABCD nội tiếp đường tròn tâm (O).
Suy ra bán kính đường tròn là OC, đường kính AC.
Hình chữ nhật ABCD có chiều dài AB = 8cm, chiều rộng BC = 6cm. Áp dụng định lý Pytago trong tam giác vuông ABC có:
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{8^2} + {6^2}} = 10cm.\)
Do đó \(R = OC = \frac{{AC}}{2} = \frac{{10}}{2} = 5cm.\)
Diện tích hình tròn là: \(\pi {R^2} = \pi {.5^2} = 25\pi (c{m^2}).\)
Diện tích hình chữ nhật là: \(8.6 = 48(c{m^2}).\)
Diện tích phần tô màu đỏ là: \(25\pi - 48 \approx 30,5(c{m^2})\) (với \(\pi \approx 3,14\)).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 77SGK Toán 9 Cánh diều
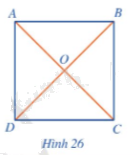
Cho hình vuông ABCD, ACcắt BDtại (O) (Hình 26).
a) Mỗi đường chéo của hình vuông ABCD có phải là đường kính của đường tròn ngoại tiếp hình vuông đó hay không?
b) Cho biết AB = a, tính OA theo a.
Phương pháp giải:
a) Mỗi hình vuông là một hình chữ nhật.
b) Áp dụng định lý Pytago trong tam giác OAB.
Lời giải chi tiết:
a) Vì hình vuông cũng là một hình chữ nhật nên mỗi đường chéo của hình vuông cũng là đường kính của đường tròn ngoại tiếp hình vuông đó.
b) Vì ABCD là hình vuông nên \(AC \bot BD\) hay \(\widehat {AOB} = 90^\circ \) và OA = OB.
Xét tam giác OAB vuông tại O, ta có:
\(\begin{array}{l}O{A^2} + O{B^2} = A{B^2}\\2O{A^2} = {a^2}\\OA = \frac{{\sqrt 2 a}}{2}.\end{array}\)
Vậy \(OA = \frac{{\sqrt 2 a}}{2}.\)
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 4 trang 77SGK Toán 9 Cánh diều
Tính tỉ số giữa chu vi của một hình vuông và chu vi của một đường tròn ngoại tiếp hình vuông đó.
Phương pháp giải:
Tính tỉ số giữa chu vi của một hình vuông và chu vi của một đường tròn ngoại tiếp hình vuông đó là: chu vi hình vuông : chu vi đường tròn.
Lời giải chi tiết:
Giả sử hình vuông có cạnh là a, thì bán kính đường tròn ngoại tiếp hình vuông đó là \(\frac{{\sqrt 2 a}}{2}.\)
Chu vi hình vuông là 4a, chu vi của đường tròn ngoại tiếp là \(2\frac{{\sqrt 2 a}}{2}\pi = \sqrt 2 a\pi .\)
Tính tỉ số giữa chu vi của một hình vuông và chu vi của một đường tròn ngoại tiếp hình vuông đó là: \(\frac{{4a}}{{\sqrt 2 a\pi }} = \frac{{2\sqrt 2 }}{\pi }.\)
Mục 3 trong SGK Toán 9 tập 2 - Cánh diều tập trung vào việc ôn tập chương về hàm số bậc nhất và hàm số bậc hai. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, cũng như củng cố kỹ năng vẽ đồ thị hàm số, tìm giao điểm của các đường thẳng và đường cong.
Bài 1 thường bao gồm các câu hỏi trắc nghiệm và bài tập tự luận về việc xác định hệ số góc, đường thẳng song song và vuông góc, cũng như ứng dụng của hàm số bậc nhất trong việc mô tả các tình huống thực tế.
Bài 2 tập trung vào việc xác định hệ số a, b, c của hàm số bậc hai, tìm đỉnh của parabol, trục đối xứng và các điểm đặc biệt. Ngoài ra, các bài tập còn yêu cầu học sinh giải phương trình bậc hai và ứng dụng các kiến thức về hàm số bậc hai để giải quyết các bài toán hình học.
Bài 3 thường đưa ra các bài toán thực tế liên quan đến việc sử dụng hàm số bậc nhất và hàm số bậc hai để mô tả các hiện tượng vật lý, kinh tế hoặc xã hội. Các bài toán này đòi hỏi học sinh phải phân tích đề bài, xây dựng mô hình toán học và giải quyết bằng các phương pháp đã học.
Ví dụ: Một vật được ném lên cao với vận tốc ban đầu là 10 m/s. Hãy viết phương trình mô tả độ cao của vật theo thời gian và tìm thời điểm vật đạt độ cao tối đa.
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 3 trang 76 và 77 SGK Toán 9 tập 2 - Cánh diều:
| Bài tập | Lời giải |
|---|---|
| Bài 1.1 | ... (Lời giải chi tiết bài 1.1) ... |
| Bài 1.2 | ... (Lời giải chi tiết bài 1.2) ... |
| Bài 2.1 | ... (Lời giải chi tiết bài 2.1) ... |
| Bài 2.2 | ... (Lời giải chi tiết bài 2.2) ... |
| Bài 3.1 | ... (Lời giải chi tiết bài 3.1) ... |
Hy vọng rằng với lời giải chi tiết và dễ hiểu này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong mục 3 trang 76, 77 SGK Toán 9 tập 2 - Cánh diều. Chúc các em học tập tốt!