Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 5 trang 41 SGK Toán 9 tập 2 - Cánh diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong các kỳ thi.
Mẫu số liệu dưới đây ghi lại độ dài quãng đường di chuyển trong 1 tuần (đơn vị: kilomet) của 60 chiếc ô tô: Ghép các số liệu trên thành 5 nhóm sau: [100; 120), [120; 140), [140; 160), [160; 180); [180; 200). a) Tìm tần số của mỗi nhóm. Lập bảng tần số ghép nhóm của mẫu số liệu ghép nhóm đó. b) Tìm tần số tương đối của mỗi nhóm đó. Lập bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó. Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột và biểu đồ đoạn thẳng của mẫu số liệu
Đề bài
Mẫu số liệu dưới đây ghi lại độ dài quãng đường di chuyển trong 1 tuần (đơn vị: kilomet) của 60 chiếc ô tô:

Ghép các số liệu trên thành 5 nhóm sau: [100; 120), [120; 140), [140; 160), [160; 180); [180; 200).
a) Tìm tần số của mỗi nhóm. Lập bảng tần số ghép nhóm của mẫu số liệu ghép nhóm đó.
b) Tìm tần số tương đối của mỗi nhóm đó. Lập bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó.
Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột và biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm đó.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Đếm số lần xuất hiện của các số liệu trong từng nửa khoảng rồi lập bảng.
b) Tính tỉ số phần trăm của mỗi tần số.
Lời giải chi tiết
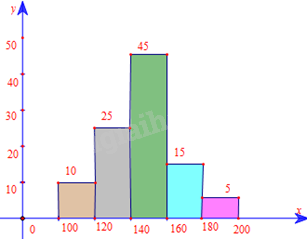
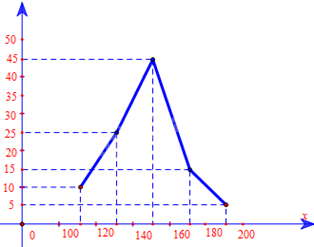
a) Tần số của mỗi nhóm: \({n_1} = 6,{n_2} = 15,{n_3} = 27,{n_4} = 9,{n_5} = 3\)

b) Tần số tương đối của các nhóm lần lượt là:
\(\begin{array}{l}{f_1} = \frac{6}{{60}}.100\% = 10\% ;{f_2} = \frac{{15}}{{60}}.100\% = 25\% ;{f_3} = \frac{{27}}{{60}}.100\% = 45\% ;\\{f_4} = \frac{9}{{60}}.100\% = 15\% ;{f_5} = \frac{3}{{60}}.100\% = 5\% \end{array}\)
Ta có bảng:

Biểu đồ cột:
Biểu đồ đoạn thẳng:
Bài tập 5 trang 41 SGK Toán 9 tập 2 - Cánh diều thuộc chương trình học Toán 9, tập trung vào việc vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Bài tập 5 thường bao gồm các dạng bài sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày một ví dụ cụ thể:
Cho hàm số y = 2x + 3. Hãy xác định hệ số góc và tung độ gốc của hàm số. Vẽ đồ thị hàm số.
Giải:
Để giải các bài tập về hàm số một cách hiệu quả, các em có thể tham khảo một số mẹo sau:
Ngoài SGK Toán 9 tập 2 - Cánh diều, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức về hàm số:
Hy vọng rằng, với hướng dẫn chi tiết và các mẹo giải bài tập hiệu quả trên đây, các em học sinh sẽ tự tin hơn trong việc giải bài tập 5 trang 41 SGK Toán 9 tập 2 - Cánh diều và các bài tập tương tự. Chúc các em học tập tốt!