Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tại giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải chi tiết và dễ hiểu cho bài tập 11 trang 67 SGK Toán 9 tập 2, thuộc chương trình Cánh diều.
Chúng tôi hiểu rằng việc tự giải bài tập đôi khi gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Cầu Trường Tiền (hay Tràng Tiền) ở thành phố Huế được khởi công vào tháng 5/1899 và khánh thành vào ngày 18/12/1900. Cầu được thiết kế theo kiến trúc Gothic, bắc qua sông Hương. Từ Festival Huế năm 2002, cầu Trường Tiền được lắp đặt một hệ thống chiếu sáng đổi màu hiệ đại. Cầu dài 402,60m gồm 6 nhịp dầm thép. Giả sử một nhịp dầm thép có dạng parabol (y = a{x^2}) trong hệ trục tọa độ Oxy, ở đó Ox song song với mặt cầu. Biết rằng hai chân nhịp dầm thép đến mặt cầu là 5,45 m (Hình 11). a) Xá
Đề bài
Cầu Trường Tiền (hay Tràng Tiền) ở thành phố Huế được khởi công vào tháng 5/1899 và khánh thành vào ngày 18/12/1900. Cầu được thiết kế theo kiến trúc Gothic, bắc qua sông Hương. Từ Festival Huế năm 2002, cầu Trường Tiền được lắp đặt một hệ thống chiếu sáng đổi màu hiệ đại. Cầu dài 402,60m gồm 6 nhịp dầm thép.
Giả sử một nhịp dầm thép có dạng parabol \(y = a{x^2}\) trong hệ trục tọa độ Oxy, ở đó Ox song song với mặt cầu. Biết rằng hai chân nhịp dầm thép đến mặt cầu là 5,45 m (Hình 11).
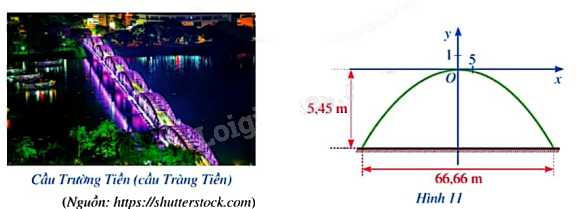
a) Xác định tọa độ của hai chân nhịp cầu trên.
b) Tìm a (làm tròn đến kết quả hàng phần nghìn).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Dựa vào hình và dữ kiện, xác định tung độ và hoành độ của 2 chân nhịp cầu.
b) Thay tọa độ 1 trong 2 điểm vừa tìm được vào hàm số\(y = a{x^2}\) để tìm a.
Lời giải chi tiết
a) Gọi tọa độ của hai chân nhịp cầu là \(\left( {{x_1};{y_1}} \right),\left( {{x_2};{y_2}} \right).\)
Vì hai chân nhịp dầm thép đến mặt cầu là 5,45 m nên tung độ của 2 chân nhịp cầu là \({y_1} = {y_2} = - 5,45.\)
Độ dài của một nhịp dầm là 66,66 m nên hoành độ của 2 chân nhịp cầu là \({x_1} = - \frac{{66,66}}{2} = - 33,33;{x_2} = \frac{{66,66}}{2} = 33,33.\)
Vậy tọa độ của hai chân nhịp cầu là \(\left( { - 33,33; - 5,45} \right),\left( {33,33; - 5,45} \right).\)
b) Vì \(\left( { - 33,33; - 5,45} \right)\) thuộc đồ thị hàm số \(y = a{x^2}\) nên ta có:
\(\begin{array}{l} - 5,45 = a{\left( {33,33} \right)^2}\\a \approx 0,005\end{array}\)
Vậy \(a \approx 0,005\).
Bài tập 11 trang 67 SGK Toán 9 tập 2 - Cánh diều thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế, cụ thể là xác định hệ số góc và đường thẳng song song.
Bài tập 11 bao gồm các ý nhỏ, yêu cầu học sinh:
Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:
Đường thẳng d1 có dạng y = 2x - 3. Vậy hệ số góc của đường thẳng d1 là a1 = 2.
Đường thẳng d2 có dạng y = -2x + 1. Vậy hệ số góc của đường thẳng d2 là a2 = -2.
Để hai đường thẳng d1 và d2 song song, chúng phải có cùng hệ số góc và khác tung độ gốc. Tuy nhiên, a1 = 2 và a2 = -2, nên a1 ≠ a2. Do đó, hai đường thẳng d1 và d2 không song song.
Để đường thẳng d3: y = (m - 1)x + 2 song song với đường thẳng d1: y = 2x - 3, ta cần có m - 1 = 2 và 2 ≠ -3. Từ m - 1 = 2, ta suy ra m = 3. Vậy với m = 3, đường thẳng d3 song song với đường thẳng d1.
Giả sử ta có hai đường thẳng: y = 3x + 1 và y = 3x - 2. Hai đường thẳng này có cùng hệ số góc là 3, nhưng khác tung độ gốc. Do đó, chúng song song với nhau.
Hãy giải các bài tập sau để củng cố kiến thức về hàm số bậc nhất và đường thẳng song song:
Bài tập 11 trang 67 SGK Toán 9 tập 2 - Cánh diều là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và đường thẳng song song. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em sẽ tự tin giải quyết bài tập này và các bài tập tương tự trong tương lai.
Chúc các em học tập tốt!