Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 122 SGK Toán 9 tập 1 - Cánh diều. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập toán học.
Bài tập này thuộc chương trình học Toán 9 tập 1, tập trung vào việc rèn luyện kỹ năng giải toán và áp dụng kiến thức đã học vào thực tế.
a) Hình 80 mô tả một phần bản vẽ của chi tiết máy. Hình đó giới hạn bởi mấy đường tròn cùng tâm? b) Hãy vẽ một hình tương tự Hình 80 bằng cách vẽ các đường tròn (left( {O;2cm} right)) và (left( {O;3cm} right)). Tính hiệu diện tích của hai hình tròn đó.
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 5 trang 122 SGK Toán 9 Cánh diều
Tính diện tích của hình vành khuyên, biết hình vành khuyên đó giới hạn bởi hai đường tròn cùng tâm và có bán kính lần lượt là 2,5cm; 2cm.
Phương pháp giải:
Dựa vào công thức tính \(S = \pi \left( {{R^2} - {r^2}} \right)\) để tính.
Lời giải chi tiết:
Diện tích hình vành khuyên đó là:
\(S = \pi \left( {2,{5^2} - {2^2}} \right) = 2,25\pi \left( {c{m^2}} \right)\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 6 trang 122SGK Toán 9 Cánh diều
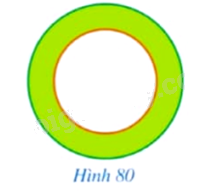
a) Hình 80 mô tả một phần bản vẽ của chi tiết máy. Hình đó giới hạn bởi mấy đường tròn cùng tâm?
b) Hãy vẽ một hình tương tự Hình 80 bằng cách vẽ các đường tròn \(\left( {O;2cm} \right)\) và \(\left( {O;3cm} \right)\). Tính hiệu diện tích của hai hình tròn đó.
Phương pháp giải:
Dựa vào hình ảnh trực quan và kiến thức đã học để trả lời câu hỏi.
Lời giải chi tiết:
a) Hình 80 được giới hạn bởi 2 đường tròn cùng tâm.
b)
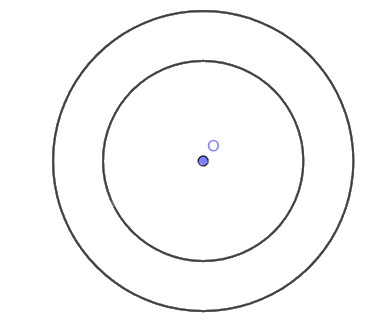
Diện tích hình tròn \(\left( {O;3cm} \right)\) là:
\(\pi {.3^2} = 9\pi \left( {c{m^2}} \right)\)
Diện tích hình tròn \(\left( {O;2cm} \right)\) là:
\(\pi {.2^2} = 4\pi \left( {c{m^2}} \right)\)
Hiệu diện tích hai hình tròn là:
\(9\pi - 4\pi = 5\pi \left( {c{m^2}} \right)\).
Video hướng dẫn giải
Trả lời câu hỏi Luyện tập 5 trang 122 SGK Toán 9 Cánh diều
Tính diện tích của hình vành khuyên, biết hình vành khuyên đó giới hạn bởi hai đường tròn cùng tâm và có bán kính lần lượt là 2,5cm; 2cm.
Phương pháp giải:
Dựa vào công thức tính \(S = \pi \left( {{R^2} - {r^2}} \right)\) để tính.
Lời giải chi tiết:
Diện tích hình vành khuyên đó là:
\(S = \pi \left( {2,{5^2} - {2^2}} \right) = 2,25\pi \left( {c{m^2}} \right)\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 6 trang 122SGK Toán 9 Cánh diều
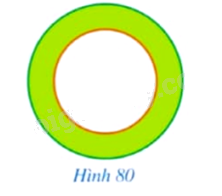
a) Hình 80 mô tả một phần bản vẽ của chi tiết máy. Hình đó giới hạn bởi mấy đường tròn cùng tâm?
b) Hãy vẽ một hình tương tự Hình 80 bằng cách vẽ các đường tròn \(\left( {O;2cm} \right)\) và \(\left( {O;3cm} \right)\). Tính hiệu diện tích của hai hình tròn đó.
Phương pháp giải:
Dựa vào hình ảnh trực quan và kiến thức đã học để trả lời câu hỏi.
Lời giải chi tiết:
a) Hình 80 được giới hạn bởi 2 đường tròn cùng tâm.
b)
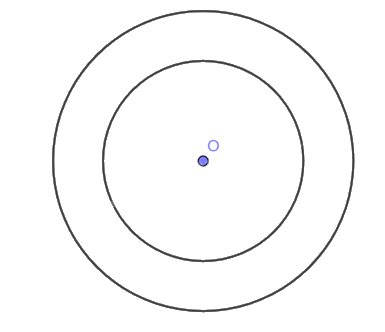
Diện tích hình tròn \(\left( {O;3cm} \right)\) là:
\(\pi {.3^2} = 9\pi \left( {c{m^2}} \right)\)
Diện tích hình tròn \(\left( {O;2cm} \right)\) là:
\(\pi {.2^2} = 4\pi \left( {c{m^2}} \right)\)
Hiệu diện tích hai hình tròn là:
\(9\pi - 4\pi = 5\pi \left( {c{m^2}} \right)\).
Mục 3 trang 122 SGK Toán 9 tập 1 - Cánh diều thường xoay quanh các bài toán liên quan đến hàm số bậc nhất, đồ thị hàm số và ứng dụng của hàm số trong việc giải quyết các bài toán thực tế. Để giải quyết hiệu quả các bài toán này, học sinh cần nắm vững các khái niệm cơ bản về hàm số, cách xác định hệ số góc và tung độ gốc, cũng như cách vẽ đồ thị hàm số.
Bài tập trong mục 3 thường bao gồm các dạng bài sau:
Cho hàm số y = 2x - 3. Hãy xác định hệ số a và b của hàm số.
Giải:
Hàm số y = 2x - 3 là hàm số bậc nhất có dạng y = ax + b. So sánh với dạng tổng quát, ta có a = 2 và b = -3.
Vẽ đồ thị của hàm số y = -x + 1.
Giải:
Để vẽ đồ thị của hàm số y = -x + 1, ta cần xác định hai điểm thuộc đồ thị. Chọn x = 0, ta có y = 1. Chọn x = 1, ta có y = 0. Vậy, đồ thị của hàm số là đường thẳng đi qua hai điểm A(0; 1) và B(1; 0).
Để giải bài tập mục 3 trang 122 SGK Toán 9 tập 1 - Cánh diều một cách hiệu quả, học sinh cần:
Ngoài SGK Toán 9 tập 1 - Cánh diều, học sinh có thể tham khảo thêm các tài liệu sau:
Giải mục 3 trang 122 SGK Toán 9 tập 1 - Cánh diều đòi hỏi học sinh phải nắm vững kiến thức cơ bản và rèn luyện kỹ năng giải toán thường xuyên. Hy vọng với hướng dẫn chi tiết và các lưu ý trên, các em sẽ tự tin giải quyết các bài tập trong mục này và đạt kết quả tốt trong môn Toán.
| Dạng bài tập | Phương pháp giải |
|---|---|
| Xác định hàm số | So sánh với dạng tổng quát y = ax + b |
| Vẽ đồ thị | Xác định hai điểm thuộc đồ thị |
| Tìm giao điểm | Giải hệ phương trình |