Chào mừng bạn đến với bài học lý thuyết về phương trình quy về phương trình bậc nhất một ẩn trong chương trình Toán 9 Cánh diều. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng quan trọng để giải quyết các bài toán liên quan.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, các dạng phương trình thường gặp và phương pháp giải chúng một cách hiệu quả.
1. Phương trình tích có dạng \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\left( {a \ne 0,c \ne 0} \right)\)
1. Phương trình tích có dạng \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\left( {a \ne 0,c \ne 0} \right)\)
Cách giải phương trình tích
Để giải phương trình tích \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\) với \(a \ne 0\) và \(c \ne 0\), ta có thể làm như sau: Bước 1.Giải hai phương trình bậc nhất: \(ax + b = 0\) và \(cx + d = 0\) Bước 2. Kết luận nghiệm: Lấy tất cả các nghiệm của hai phương trình bậc nhất vừa giải được ở Bước 1. |
Ví dụ 1:Giải phương trình \(\left( {2x + 1} \right)\left( {3x - 1} \right) = 0\)
Lời giải:
Để giải phương trình \(\left( {2x + 1} \right)\left( {3x - 1} \right) = 0\), ta giải hai phương trình sau:
*) \(2x + 1 = 0\)
\(2x = - 1\)
\(x = - \frac{1}{2}\).
*) \(3x - 1 = 0\)
\(3x = 1\)
\(x = \frac{1}{3}\).
Vậy phương trình đã cho có hai nghiệm là \(x = - \frac{1}{2}\) và \(x = \frac{1}{3}\).
Ví dụ 2: Giải phương trình \({x^2} - x = - 2x + 2\).
Lời giải:
Biến đổi phương trình đã cho về phương trình tích như sau:
\(\begin{array}{l}{x^2} - x = - 2x + 2\\{x^2} - x + 2x - 2 = 0\\x\left( {x - 1} \right) + 2\left( {x - 1} \right) = 0\\\left( {x + 2} \right)\left( {x - 1} \right) = 0.\end{array}\)
Ta giải hai phương trình sau:
*) \(x + 2 = 0\)
\(x = - 2\).
*) \(x - 1 = 0\)
\(x = 1\).
Vậy phương trình đã cho có hai nghiệm là \(x = - 2\) và \(x = 1\).
2. Phương trình chứa ẩn ở mẫu
Điều kiện xác định của phương trình chứa ẩn ở mẫu
Trong phương trình chứa ẩn ở mẫu, điều kiện của ẩn để tất cả các mẫu thức trong phương trình đều khác 0 được gọi là điều kiện xác định của phương trình. |
Ví dụ:
- Phương trình \(\frac{{5x + 2}}{{x - 1}} = 0\) có điều kiện xác định là \(x - 1 \ne 0\) hay \(x \ne 1\).
- Phương trình \(\frac{1}{{x + 1}} = 1 + \frac{1}{{x - 2}}\) có điều kiện xác định là \(x + 1 \ne 0\) và \(x - 2 \ne 0\) hay \(x \ne - 1\) và \(x \ne 2\).
Các bước giải phương trình chứa ẩn ở mẫu
Bước 1.Tìm điều kiện xác định của phương trình. Bước 2. Quy đồng mẫu thức hai vế của phương trình rồi khử mẫu. Bước 3.Giải phương trình vừa tìm được. Bước 4. Kết luận nghiệm: Trong các giá trị tìm được ở Bước 3, các giá trị thỏa mãn điều kiện xác định chính là nghiệm của phương trình đã cho. |
Ví dụ: Giải phương trình \(\frac{2}{{x + 1}} + \frac{1}{{x - 2}} = \frac{3}{{\left( {x + 1} \right)\left( {x - 2} \right)}}\)
Lời giải:
Điều kiện xác định \(x \ne - 1\) và \(x \ne 2\).
\(\frac{2}{{x + 1}} + \frac{1}{{x - 2}} = \frac{3}{{\left( {x + 1} \right)\left( {x - 2} \right)}}\)
\(\frac{{2\left( {x - 2} \right) + \left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x - 2} \right)}} = \frac{3}{{\left( {x + 1} \right)\left( {x - 2} \right)}}\)
\(2\left( {x - 2} \right) + \left( {x + 1} \right) = 3\).
\(\begin{array}{l}2\left( {x - 2} \right) + \left( {x + 1} \right) = 3\\2x - 4 + x + 1 = 3\\3x - 3 = 3\\3x = 6\\x = 2\end{array}\)
Ta thấy \(x = 2\) không thỏa mãn điều kiện xác định của phương trình.
Vậy phương trình \(\frac{2}{{x + 1}} + \frac{1}{{x - 2}} = \frac{3}{{\left( {x + 1} \right)\left( {x - 2} \right)}}\) vô nghiệm.
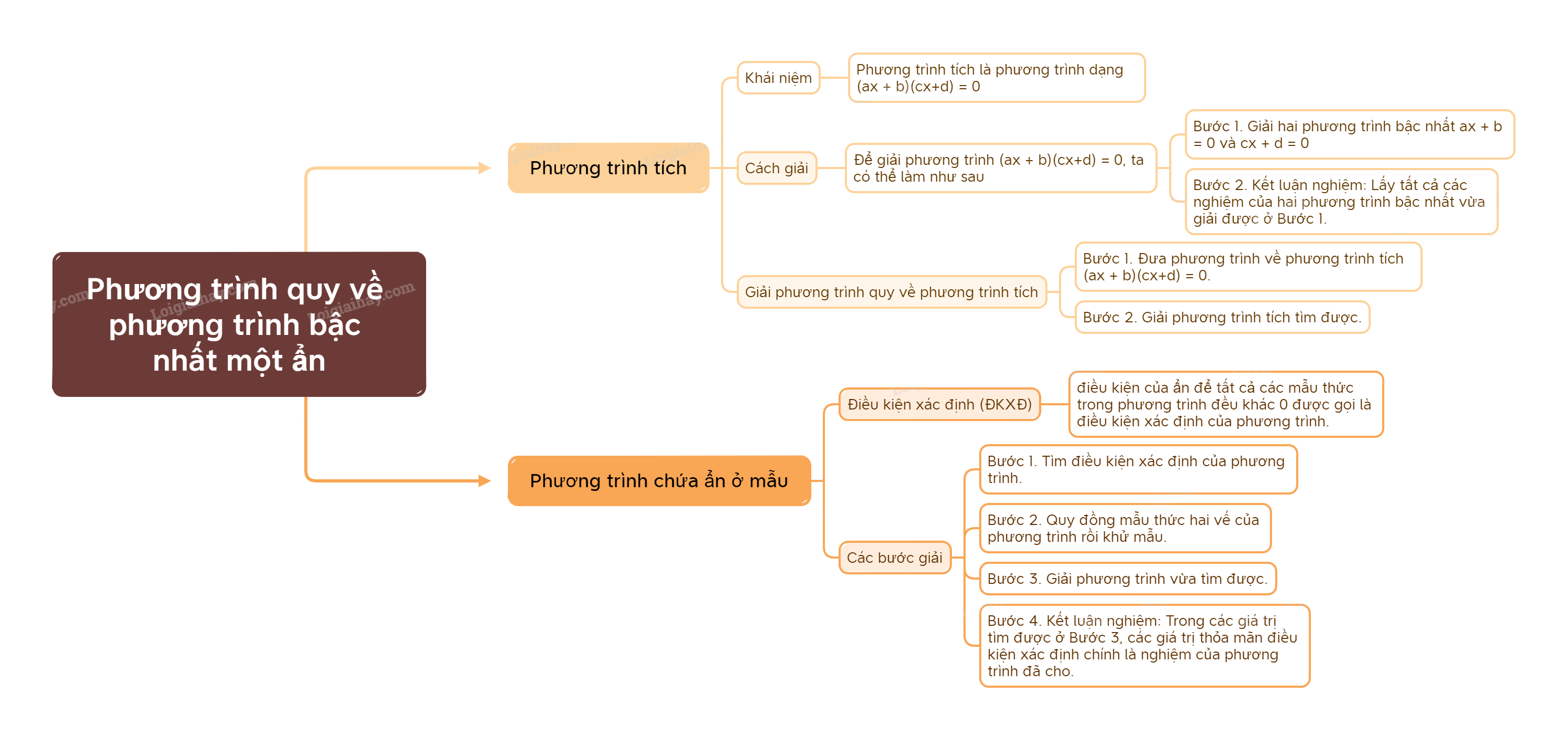
Trong chương trình Toán 9, việc nắm vững kiến thức về phương trình là vô cùng quan trọng. Một trong những dạng phương trình thường gặp là phương trình quy về phương trình bậc nhất một ẩn. Bài viết này sẽ cung cấp một cách chi tiết và dễ hiểu về lý thuyết của dạng phương trình này, đặc biệt dành cho học sinh sử dụng sách Cánh diều.
Phương trình quy về phương trình bậc nhất một ẩn là phương trình mà sau khi thực hiện các phép biến đổi đại số (như khử mẫu, bỏ ngoặc, chuyển vế, rút gọn), ta thu được một phương trình có dạng:
ax + b = 0
Trong đó:
Có nhiều dạng phương trình có thể quy về phương trình bậc nhất một ẩn. Dưới đây là một số dạng phổ biến:
Để giải phương trình chứa mẫu số, ta cần tìm điều kiện xác định (ĐKXĐ) của phương trình. Sau đó, ta quy đồng mẫu số và khử mẫu. Cuối cùng, ta giải phương trình bậc nhất một ẩn thu được.
Ví dụ:
Giải phương trình:1/x + 2 = 3/x
Để giải phương trình chứa ngoặc, ta cần bỏ ngoặc bằng cách nhân phân phối hoặc sử dụng các quy tắc về dấu ngoặc. Sau đó, ta giải phương trình bậc nhất một ẩn thu được.
Ví dụ:
Giải phương trình:2(x - 1) + 3 = 5
Phương trình tích có dạng: A(x) * B(x) = 0. Phương trình này tương đương với A(x) = 0 hoặc B(x) = 0.
Ví dụ:
Giải phương trình:(x - 2)(x + 3) = 0
Để giải phương trình bậc nhất một ẩn ax + b = 0, ta thực hiện các bước sau:
Hãy tự giải các bài tập sau để củng cố kiến thức:
Việc hiểu rõ lý thuyết và phương pháp giải phương trình quy về phương trình bậc nhất một ẩn là nền tảng quan trọng để học tốt môn Toán 9. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải các bài toán.